Premier exemple : le jeu de la vie
J’utilise le composant RecGrid (Vector/Grid) pour créer une grille rectangulaire où le nombre de cellules est ajusté d’un curseur en nombres entiers et la longueur et la largeur des cellules d’un autre curseur en nombres réels. Je crée une surface à l’aide du composant Boundary Surface (Surface/Freeform).
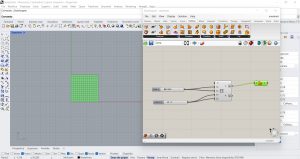
Par conséquent, j’impose l’état initial d’entrée de toutes les cellules à zéro, donc nous supposons que toutes les cellules sont mortes au début du processus. J’insère un composant Lng (Set/List) qui calcule le nombre de cellules de la grille. Grâce à un composant Repeat (Set/Sequence) et à un composant Panel (Params/Input), j’associe à chaque cellule la valeur zéro. En tant que sortie du composant Repeat, j’obtiens une liste de nombres associés à la valeur zéro. Nous choisissons maintenant quatre cellules à considérer comme vivantes, cellules que nous identifierons en raison de leur position en termes de lignes et de colonnes. J’insère le composant Replace (Set/List) lié à un Panel avec une valeur de 1 pour remplacer la valeur de ces 4 cellules vivantes de zéro à 1. Je le branche à un composant Expression (Maths/Script) qui me permettra d’identifier la position des cellules en fonction des coordonnées d’entrée que je saisis grâce à l’utilisation de Slider, le tout toujours par rapport à la longueur L des cellules.
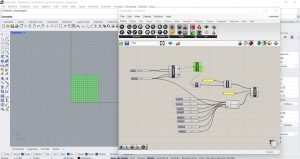
Nous devons maintenant identifier les cellules mortes avec la couleur noire et les cellules vivantes avec la couleur jaune et pour cela j’utilise un composant Custom Preview (Display/Preview) que nous relions à la liste des supérieure créées par le composant Boundary. Nous introduisons deux composants Swatch Color (Params/Input) que nous associons respectivement à la couleur noire et à la couleur jaune. Nous connectons ces composants à l’entrée du composant Item (Set/List) dont le rôle sera d’associer le zéro à la couleur noire et l’un à la couleur jaune, en le connectant au composant Preview nous pourrions obtenir le résultat que nous recherchions.
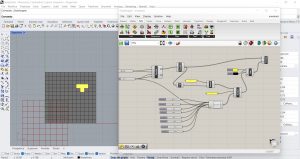
Application des règles du jeu de la vie
Pour appliquer les règles du jeu de la vie, nous devons programmer un de nos composants avec le langage Python, en insérant le composant Python (Maths/Script). Je change les variables d’entrée du composant de X et Y en C et N et je les divise en listes de nombres entiers. Dans C, il y aura la liste des états des cellules et dans N la liste des sommes des états des 8 cellules adjacentes d’une cellule. Maintenant, vous devez programmer le composant en gardant toujours à l’esprit que C indique l’état d’une cellule et N combien des 8 cellules voisines sont vivantes. Nous allons donc définir que si l’état de la cellule est vivant et a deux ou trois cellules vivantes à proximité, il continuera à vivre, si c’est une cellule morte qui a trois cellules vivantes à proximité, il deviendra vivant. Dans toutes les autres situations, elle continue d’être morte ou meurt. Ce processus doit être cyclique et basé sur les cycles précédents.
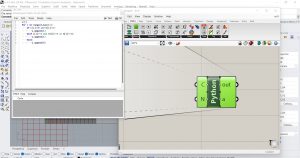
Pour calculer le nombre de cellules vivantes à proximité d’une cellule, nous utilisons le composant Proximity 2D (Mesh/Triangulation) qui permet de récupérer des points dans une zone donnée autour du point choisi. Nous l’utiliserons pour récupérer le centre des 8 cellules adjacentes à la cellule choisie. Le centre de la cellule est calculé à partir du composant Surface (Surface/Analysis) qui a le centre comme sortie C. J’insère un curseur pour indiquer que le composant Proximity doit récupérer les 8 centres des cellules les plus proches et deux curseurs pour indiquer la zone dans laquelle il doit chercher. Je relie la sortie de Proximity à un composant List Item que je relierai à son tour à un composant MA (Maths/Operator) qui fait la somme des états des cellules voisines. À la fin, je connecte au composant Python. Je dois maintenant installer le mécanisme récursif pour que la sortie du composant Python devienne l’entrée pour la prochaine boucle. J’ai connecté les composants Loop Start et Loop End d’Anemone aux paramètres restants que j’avais déjà entrés et j’ai obtenu les différentes étapes requises. J’ai essayé de faire la même chose avec Hoop Snake et j’ai obtenu le même résultat.
Toutes les différentes étapes





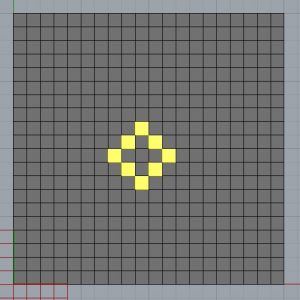

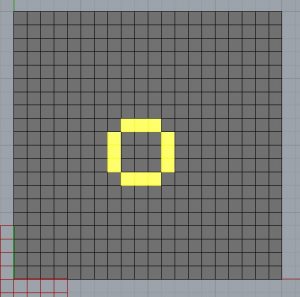


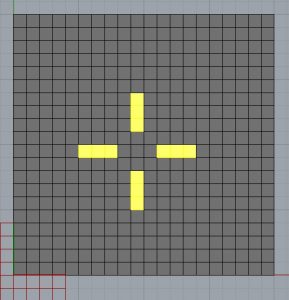

Initialiser la grille au hasard
Dans ce cas, je ne sectionne plus la position de départ des premières cellules vivantes. Je place un composant Jitter (Sets/Sequence) que je relie à l’out du composant Repeat auquel j’ai ajouté un Panel à l’entrée D. Je place un slider à l’entrée S du Jitter pour contrôler l’effet aléatoire. J’ai essayé Anemone et Hoop Snake.
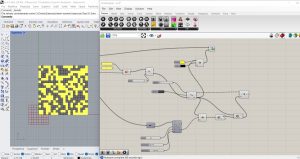
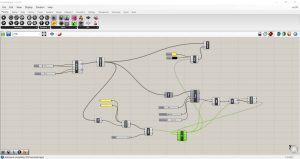


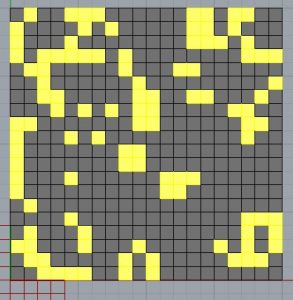
J’ai changé les valeurs de G, R- et R+ et j’ai obtenu plusieurs configurations marquées cette fois avec les couleurs noir et rouge.

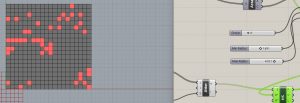
J’ai essayé de changer le langage Python. J’ai fait le Night and Day en partant d’une base causale et non d’un nombre fixe de cellules vivantes de départ avec une position spécifique.
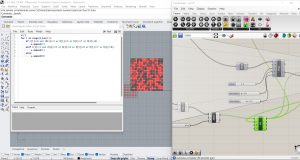
J’ai fait pareil pour High Life et l’immigration.
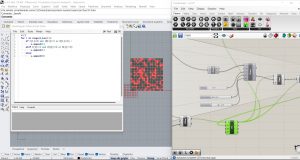
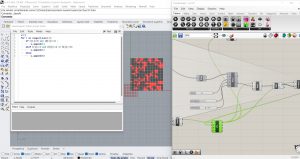
Sans initialiser la grille au hasard mais avec les 4 cellules de départ vivant dans les positions préétablies j’ai obtenu pour la High Life pour le Jour et la Nuit et pour l’Immigration ces résultats.

1 comment
François Guéna says:
Jun 8, 2022
Très bon travail.