Exercise 6: Géométrie fractale – partie 1

La géométrie fractal : C’est un objet géométrique « infiniment morcelé » dont des détails sont observables à une échelle arbitrairement choisie et le but de ce cours c’est d’apprendre à faire des courbes fractales.

Exercice 1 : La courbe du crabe

Afin de créer cette géométrie, on va utiliser : Axiome est un segment de droite D dont l’origine est S et l’extrémité E et le règle de substitution, il s’agit de d’appliquer à la ligne 2 similitudes de rapport Racine de 2 / 2 et d’angle pi/4 et -pi/4 centrées sur S pour l’une et sur E pour l’autre.

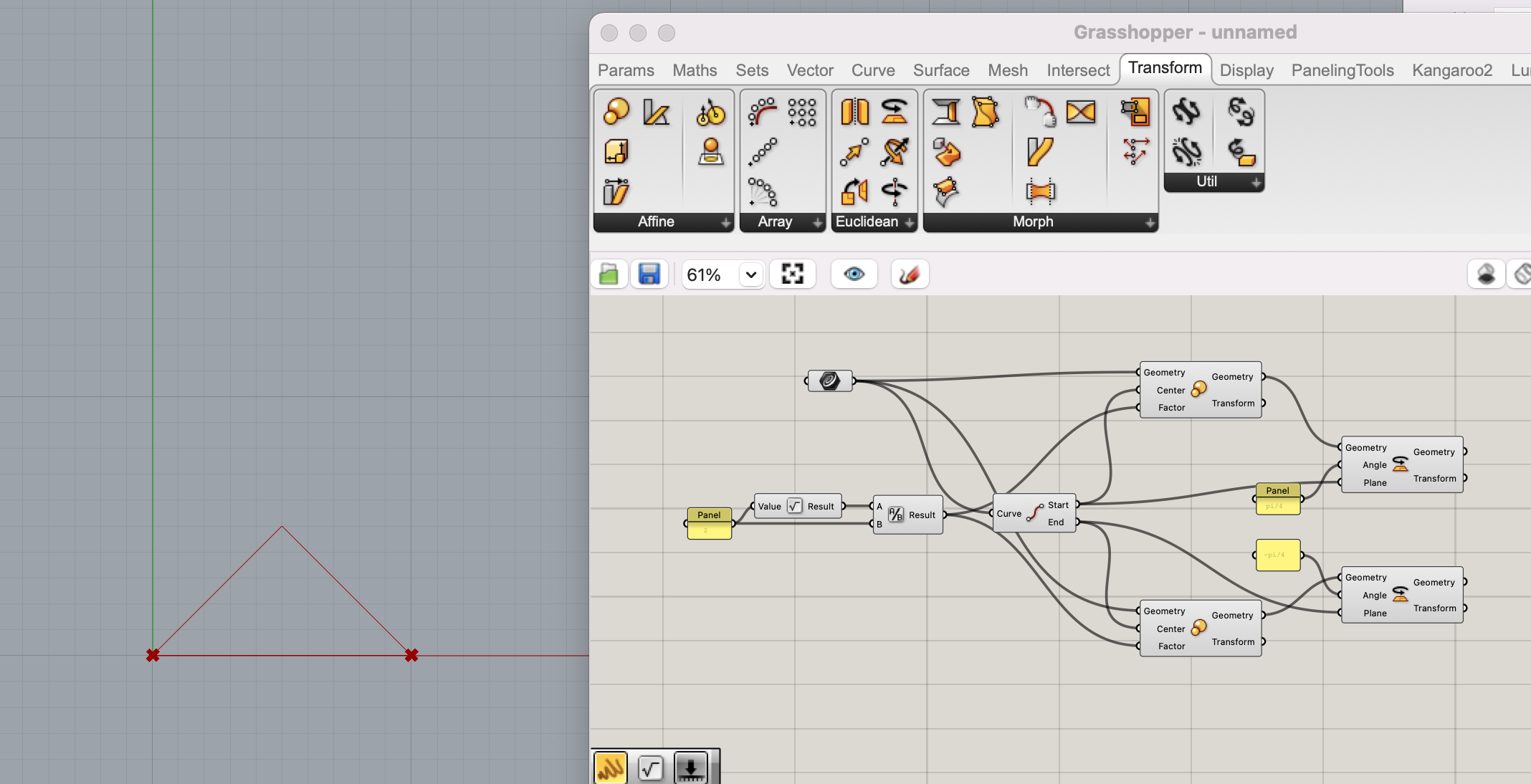
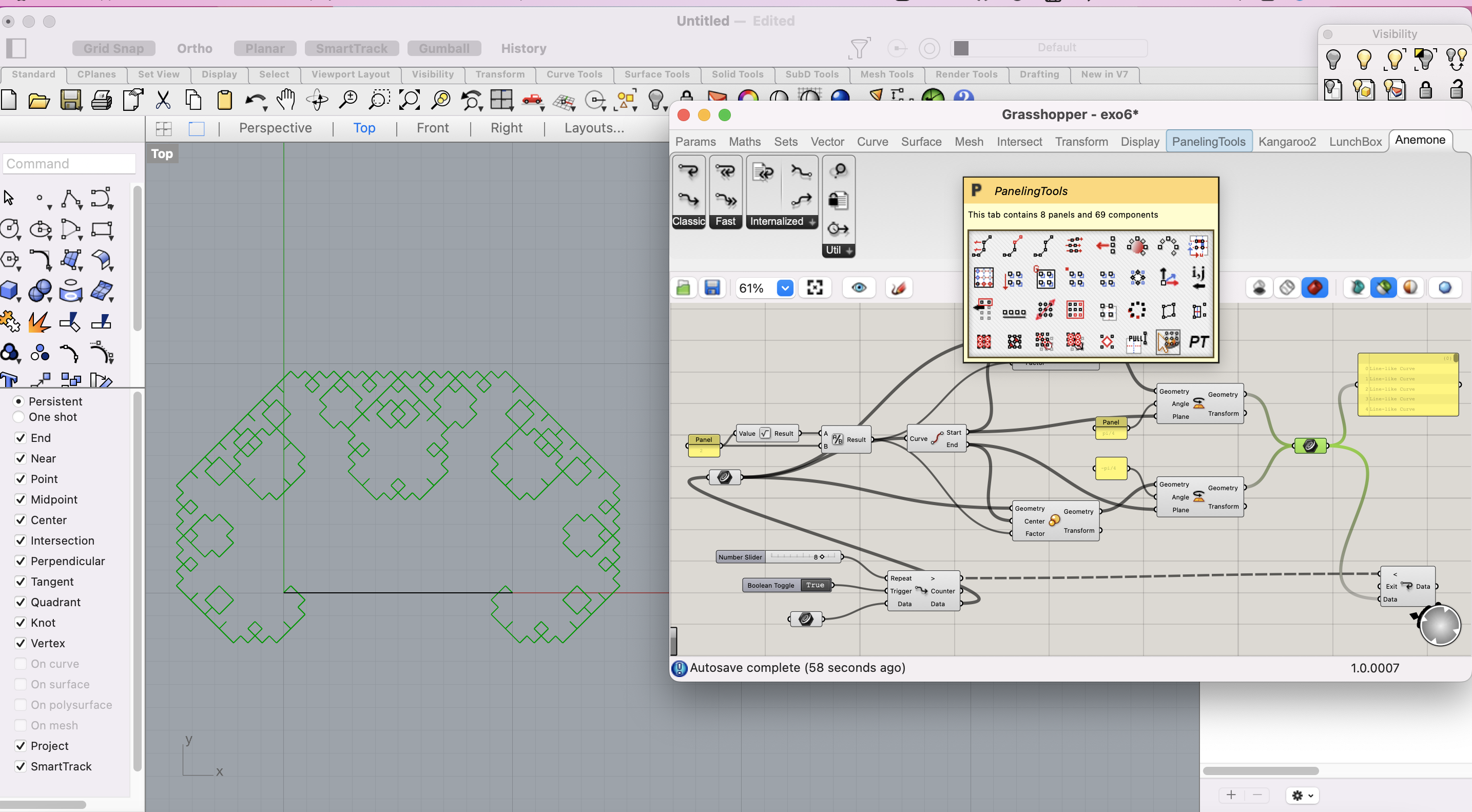
On télécharge le plugin Anemone, qui nous permettra de contrôler une application récursive. On va insérer un composant LoopStart (Anemone/Class/LoorStart) et un composant LoopEnd (Anemone/Class/LoorEnd), afin d’indiquer le début et la fin de l’opération récursive. On va placer le paramètre booléen (Params/Input/Button) afin de pouvoir réinitialiser le traitement récursif. En ajoutant un slider on peut contrôler le nombre entier d’itérations.

Exemple 2 : La courbe du dragon

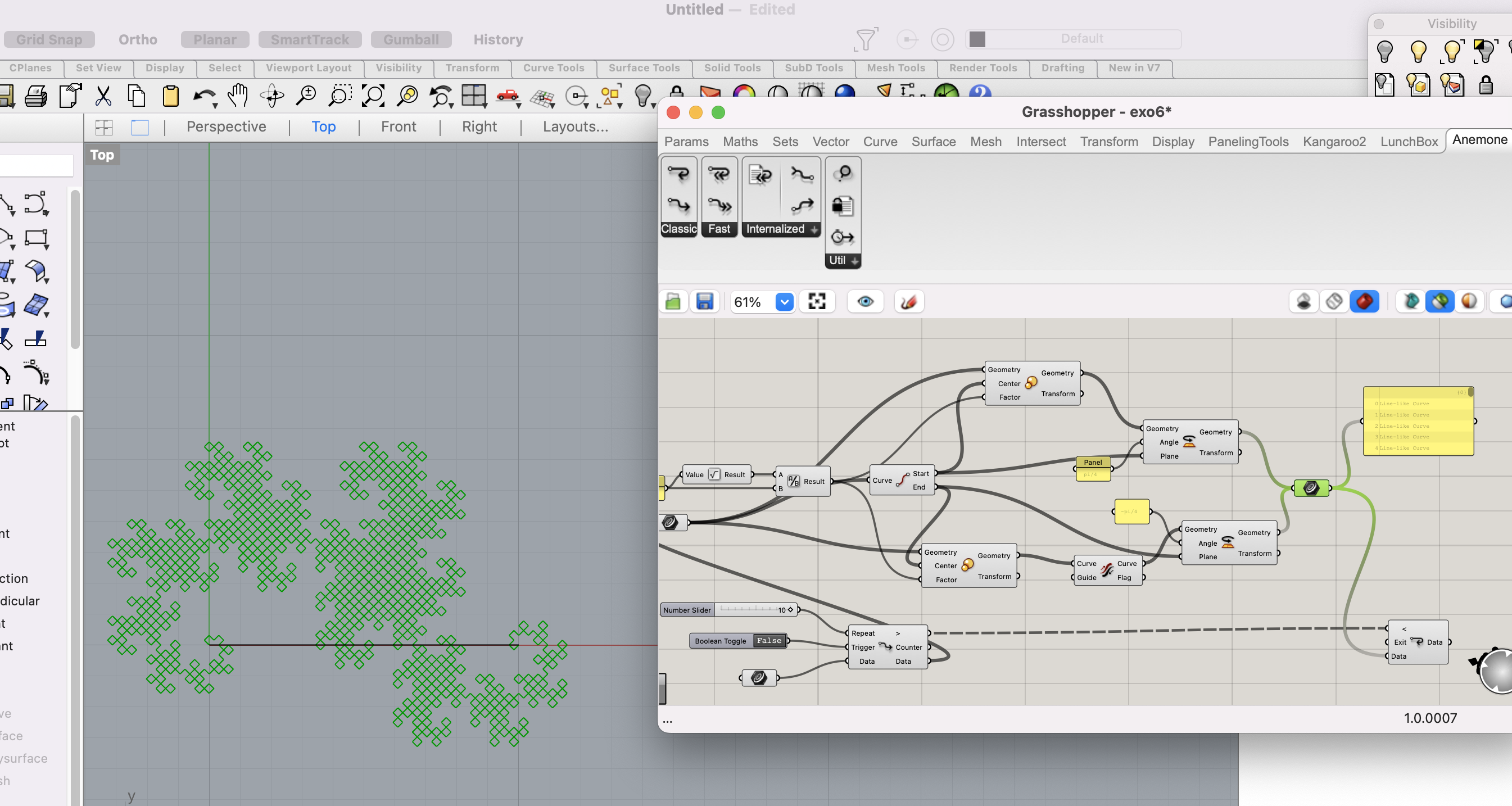
Dans cet exemple on va appliquer à la ligne 2 similitudes de rapport racine de 2/2 et d’angle pi/4 et -pi/4, ainsi on va inverser la deuxième ligne générée.

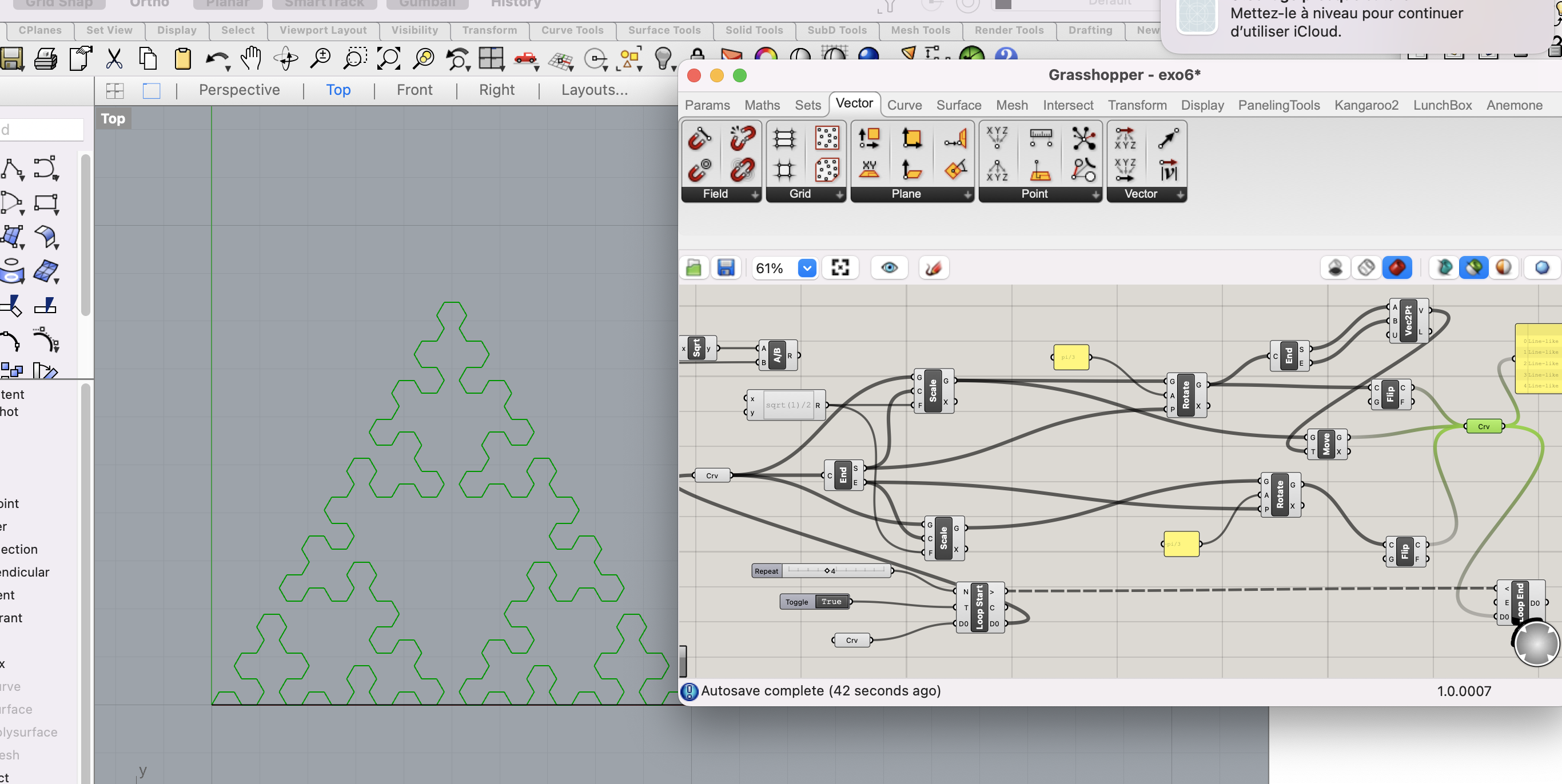
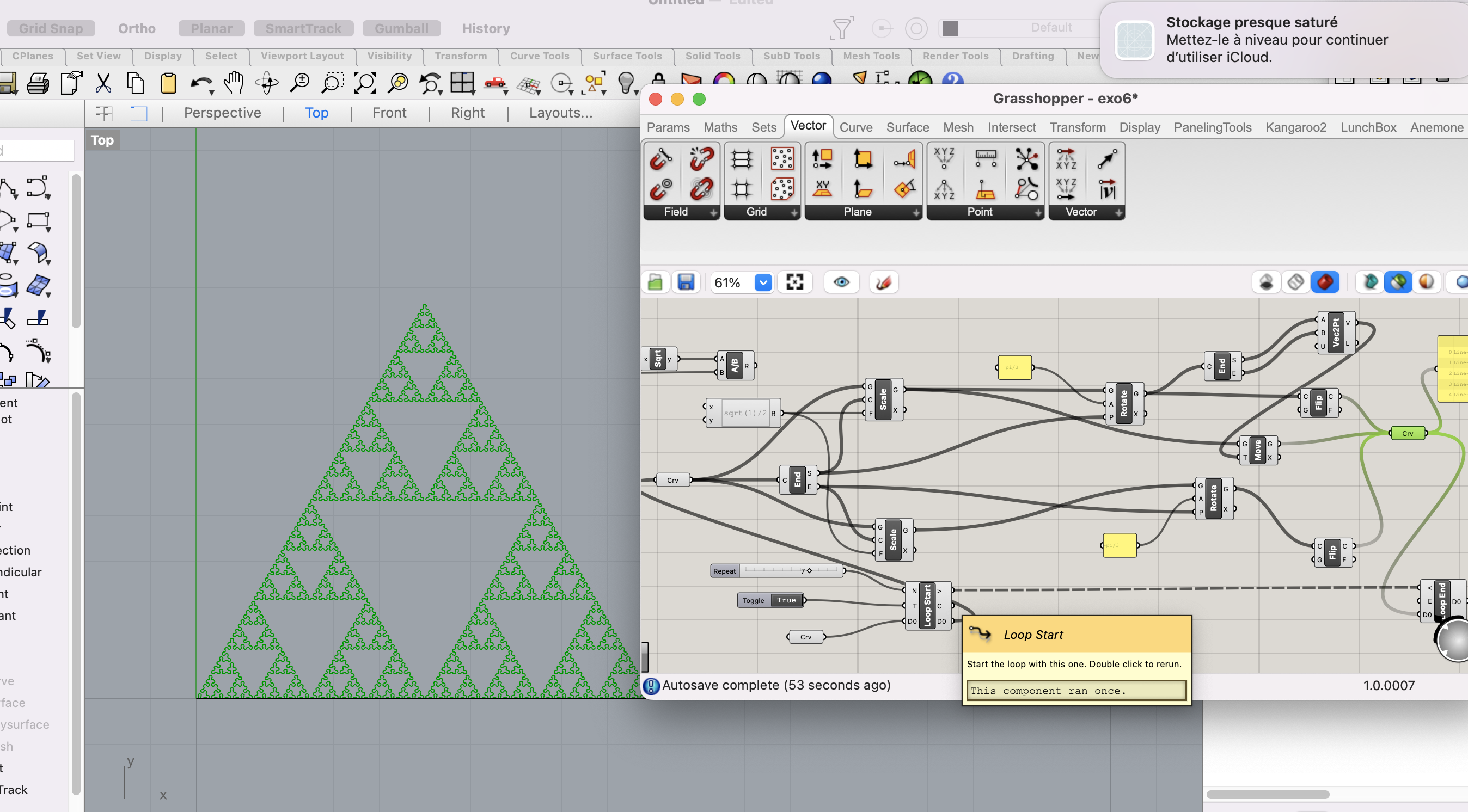
Exemple 3 : La courbe du Sierpinsky

Ces ensembles de transformations applicables récursivement sur les éléments d’un objet produisent des géométries nouvelles et complexes.

L’utilisation de la géométrie fractale, je trouve intéressant pour la fabrication du des éléments de façades comme une moucharabieh ou bien pour créer des espaces, des structures portantes, des façades biomimétiques et bien plus.