A travers ces exemples et exercices, on va appliquer le principe de la géométrie fractale aux surfaces et aux solides. On va ainsi utiliser L-Systems afin de produire des objets fractals.
Application à des surfaces :
Dans cet exemple, on va créer une règle afin de l’appliaquer à une surface triangulaire :
- Etape 1
On commence par créer une surface triangulaire dans Rhino.
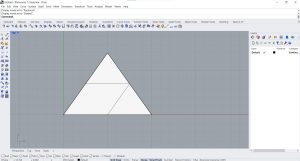
- Etape 2
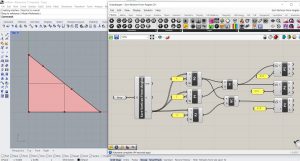
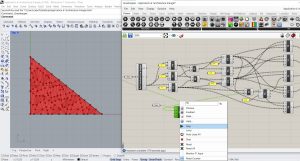
Par la suite, on va appliquer 3 transformations homothétiques du triangle. Dans Grasshopper, on va placer un paramètre Surface et l’associer à la surface créée en Rhino. Ainsi, grâce au paramètre Deconstruct Brep, on va retourner la liste des sommets et la liste des arêtes. En plaçant un composant Scale, on applique des transformations homothétiques.
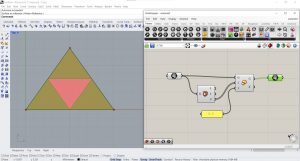
- Etape 3
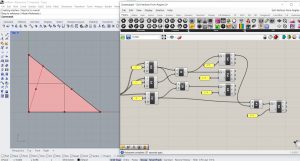
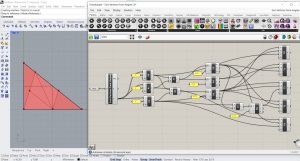
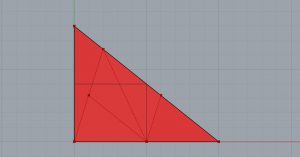
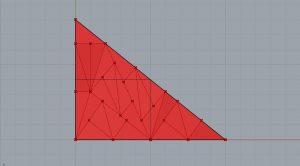
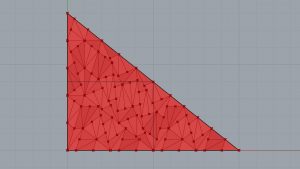
On va ajouter d’abord les paramètres LoopStart et LoopEnd, afin de créer un mécanisme récursif. Ensuite, on va ajouter un Number Slider comprenant des nombres entiers entre 0 et 10, ce qui nous permettra de contrôler le nombre d’itérations. On va aussi ajouter le paramètre Bouton et le relier au composant LoopStart. Ainsi, on fera attention à intégrer le symbole Graft dans l’entrée G du paramètre Scale. Ensuite, on va relier la sortie > du composant LoopStart à l’entrée < du composant LoopEnd. Le Number Slider nous permet de varier le nombre d’itérations.
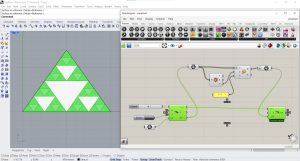
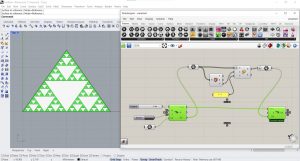

Exercice 1
Pour cet exercice, on va modifier le programme précédent. Ici, un polygone régulier de cotés 5,6,7 ou 8, sera le motif de départ. On va créer en Grasshopper un un polygone régulier, en appliquant le paramètre Polygone et en lui attribuant un Number Slider afin de pouvoir modifier le nombre de cotés. Ainsi, on va transformer ce polygone en surface, en ajoutant le paramètre Boundary Surfaces.
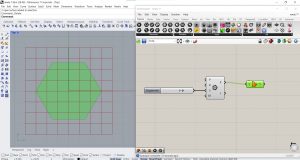
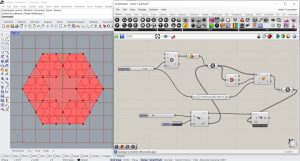
Ensuite, dans Scale, on va modifier le rapport d’homothétie, en ajoutant le composant Expression et lui attribuant la formule : 1/(4*cos(pi/S)²). Pour ce composant, on va d’abord, renommer la variable x en S, ensuite supprimer la variable y. On va relier la sortie de l’expression à l’entrée F du composant Scale.
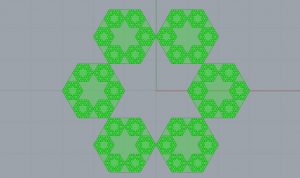
Application à des objets 3D
- Le cube de Sierpinski
Afin de créer le cube de Sierpinski, on va partir du programme Grasshopper du triangle de Sierpinski. D’abord, on va créer en Rhino un cube et l’associer au paramètre Brep.
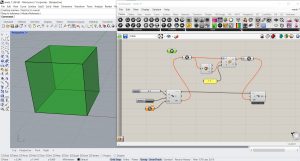
On va ajouter un deuxième composant Scale et le relier à l’entrée G au paramètre Brep d’entrée de la règle. Ensuite, on ajoute un paramètre Point on Curve, on va associer son entrée à la sortie E du composant Brep. On ne modifie pas la valeur du composant Point on Curve, car il est correspond déjà au milieu de la courbe.
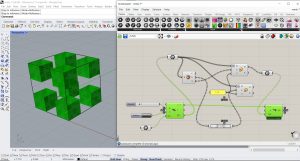
En oubliant de relier le composant Scale au paramètre Brep, j’ai obtenu ce résultat :

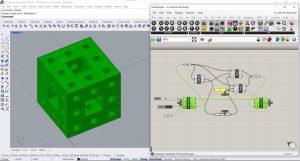
Voici le résultat final :
Application à l’architecture
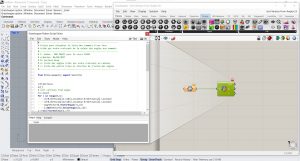
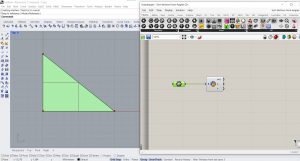
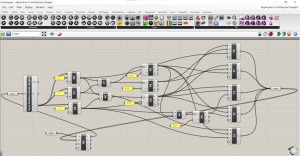

Créer le L-System avec Grasshopper
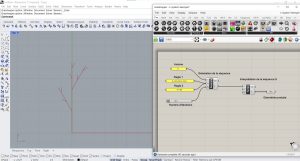
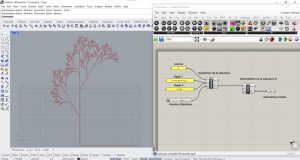
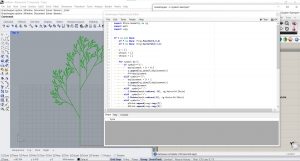
Adapter le graphe et le script à d’autres L-System
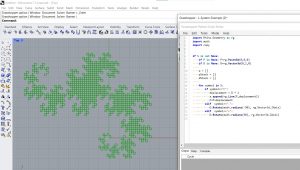
- La courbe de Koch
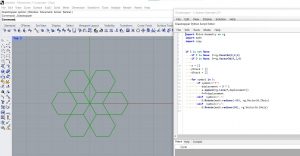
- Combination of Islands and Lakes
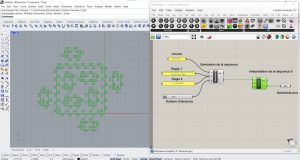
Voici quelques exercices utilisant L-systems :
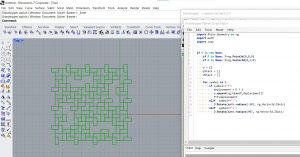
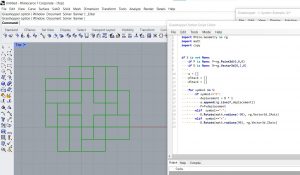
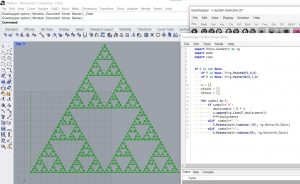

1 comment
François Guéna says:
Jun 1, 2022
Très bon travail. Tout semble avoir été compris pour ce cours sur les géométries fractales