Exercise 10 – Automates cellulaires 2

Application d’un automate cellulaire à une surface

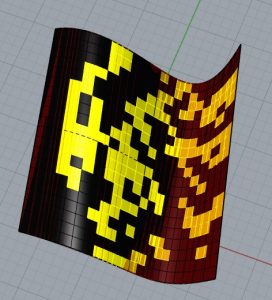
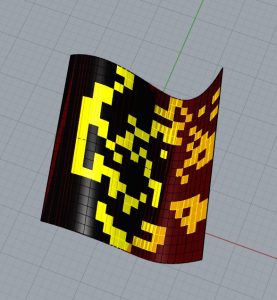
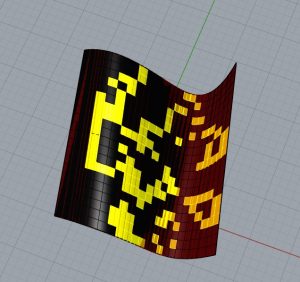
Pour commencer, je vais prendre le fichier de la leçon précédente. J’entre un paramètre Surface (Params/Geometry) qui aura comme entrée une surface non plane créée dans Rhino. Je le branche au paramètre Divide Domain 2 (Maths/Domain) qui ajustera les dimensions des sous-surfaces qui constitueront notre surface non plane et donc nos cellules. Je connecte le paramètre Surface et le pramatro Divide au paramètre SubSurf (Surface/Util/Isotrim) qui ramène à la sortie S la liste des sous-surfaces et donc des cellules. Je relie cette partie à tout le reste du diagramme que j’avais obtenu de la dernière leçon. J’ai créé une surface non plane dans Rhino et je l’ai associée au paramètre Surface. C’est ainsi que j’ai pu appliquer le dessin de l’automate cellulaire sur ma surface. Je rapporte les images des premiers passages puis il devient récursif.

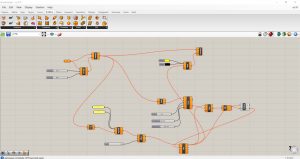
J’ai créé une surface non plane dans Rhino et je l’ai associée au paramètre Surface. C’est ainsi que j’ai pu appliquer le dessin de l’automate cellulaire sur ma surface. Je rapporte les images des premiers passages puis il devient récursif.

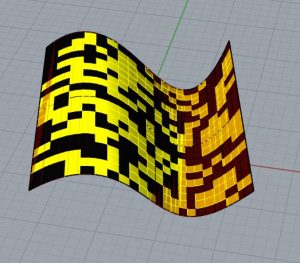
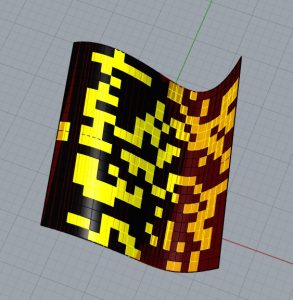
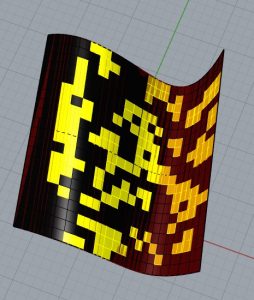
Modification des règles

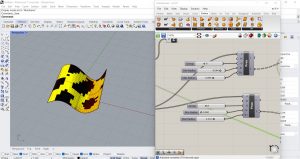
Nous créons maintenant un nouvel automate cellulaire en dupliquant le code existant pour inspecter deux zones concentriques différentes au lieu d’une seule qui correspondent respectivement au quartier le plus proche et au quartier le plus éloigné. Nous allons insérer une nouvelle loi sur Python : Quel que soit l’état actuel de la cellule dont vous voulez connaître l’état dans la prochaine génération, si le nombre de cellules vivantes voisines de la première zone est supérieur à celui de la deuxième zone, alors la cellule sera morte dans la prochaine génération, sinon elle sera vivante. Je modifie le langage du composant Python pour que l’énoncé se produise, puis je duplique les composants de règle afin de pouvoir ajuster la variable Y ajoutée, puis le rayon de la zone de contrôle ajoutée. Plusieurs configurations sont obtenues ci-dessous.

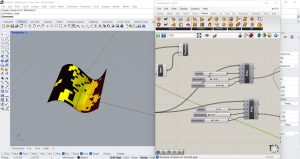
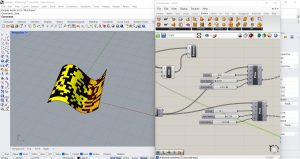
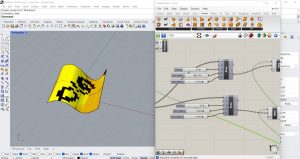
Exercises

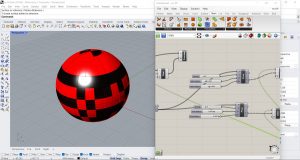
J’ai donc essayé de changer de surface et de modifier la taille des cellules, dans ce cas j’ai choisi une sphère avec les cellules rectangulaires. J’ai également changé les couleurs pour mieux distinguer l’exercice du reste de la leçon. Pour utiliser les billes, j’ai dû remplacer le paramètre Proximity 2D par le paramètre Proximity 3D (Mesh/Triangulation).

Voici quelques résultats.

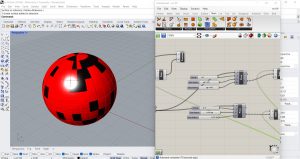
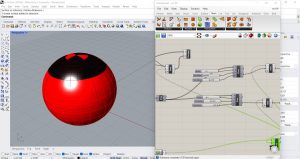
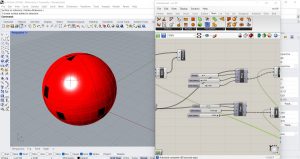
J’ai ensuite inversé le langage Python en écrivant X(i)<Y(i) et en gardant les mêmes valeurs, je voulais voir ce qui changeait.

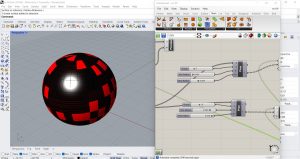
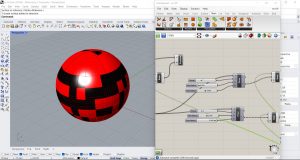
Réaliser un automate cellulaire 3D

Je connecte un curseur à trois composants Series (Sets/Sequence) pour générer des listes de nombres comprises entre 0 et le nombre indiqué par le curseur. Le composant CrossRef (iSets/List/Cross Reference) constituera le produit cartésien des 3 listes et donc à générer les combinaisons possibles des valeurs des 3 listes. Après avoir obtenu de cette façon toutes les coordonnées des centres des cellules, j’insère le composant Point (Vector/Point/Construct Point) qui créera la liste de tous les points correspondant aux centres des cellules. Enfin, le composant Box (Surface/Primitive/Center Box) créera des cubes centrés sur tous les points choisis.

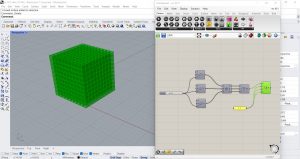
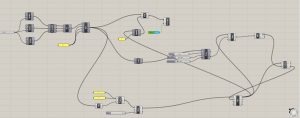
L’initialisation est identique à celle que nous avons déjà utilisée pour les automates cellulaires où, parmi les cubes créés, nous choisissons un nombre aléatoire comme cellules vivantes. Nous calculons ensuite le nombre de cellules vivantes voisines qui l’entourent en utilisant dans ce cas le composant Proximity 3D (Mesh/Triangulation). Le code Python est identique à celui qui est présent dans le jeu de la vie. Dans ce cas, nous décidons de ne pas montrer les cellules mortes et de ne montrer que les cellules vivantes. Je place ensuite un composant Equals (Maths/Operator) qui compare les états des cellules avec 0 et crée une liste de valeurs booléennes. Le composant Cull (Sets/Sequence) supprime les éléments ayant une valeur False de la liste.