Cours 7: Géométrie fractale 2

Application à des surfaces

exemple: Le triangle de Sierpinsky

Le travail consiste à suivre la logique du cours précédent mais sur une surface au lieu d’une ligne pour cela j’ai suit les étapes suivantes indiquées dans le cours:

• Construire une surface triangulaire dans la scène Rhino grace à l’outil « Surface from 3 or 4 corner points »

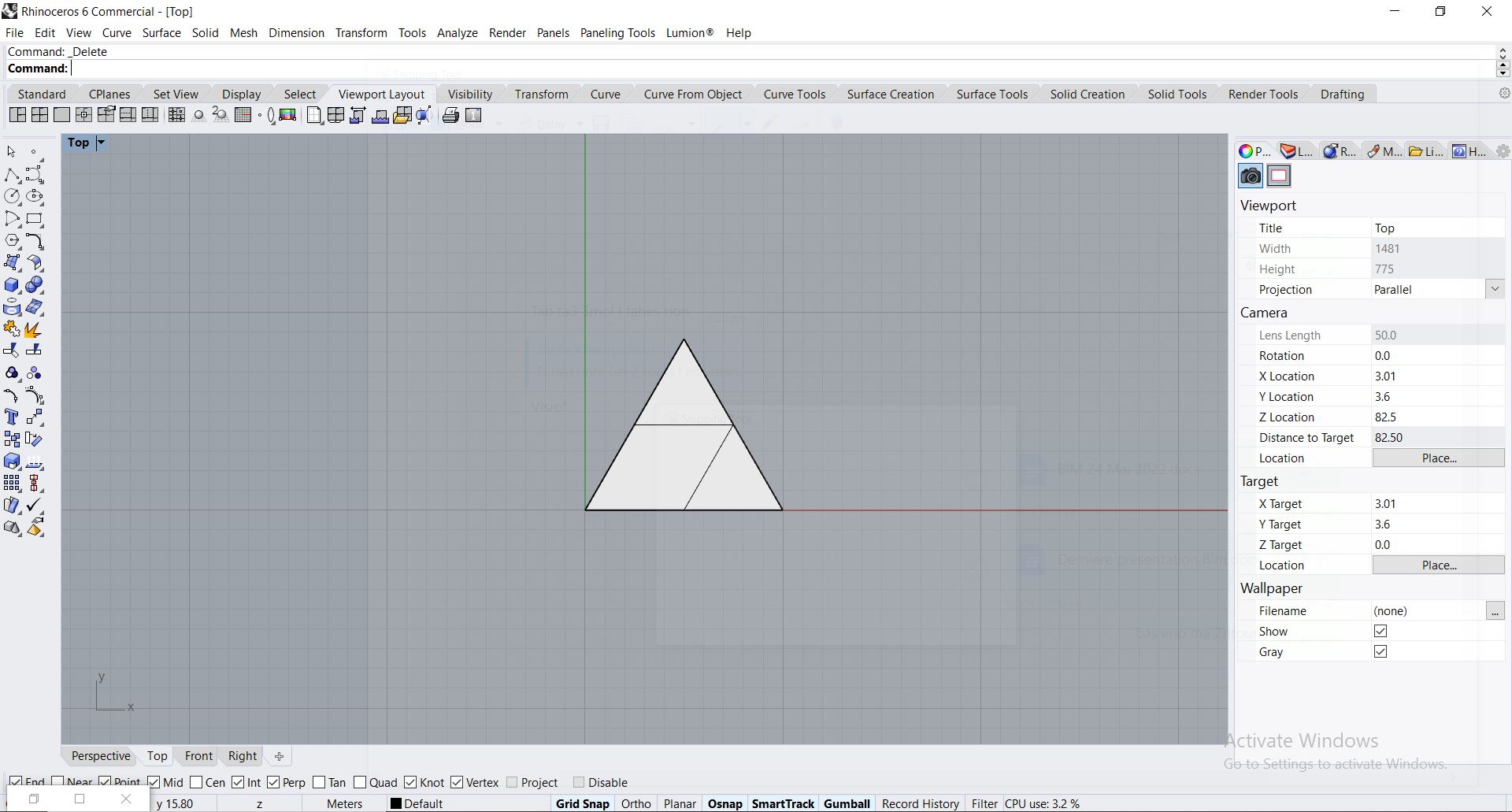
• Construire le programme visuel de la règle de substitution.

Ca consiste à appliquer 3 transformations homothétiques pour obtenir 3 triangles centrées sur chacun de ses sommets.

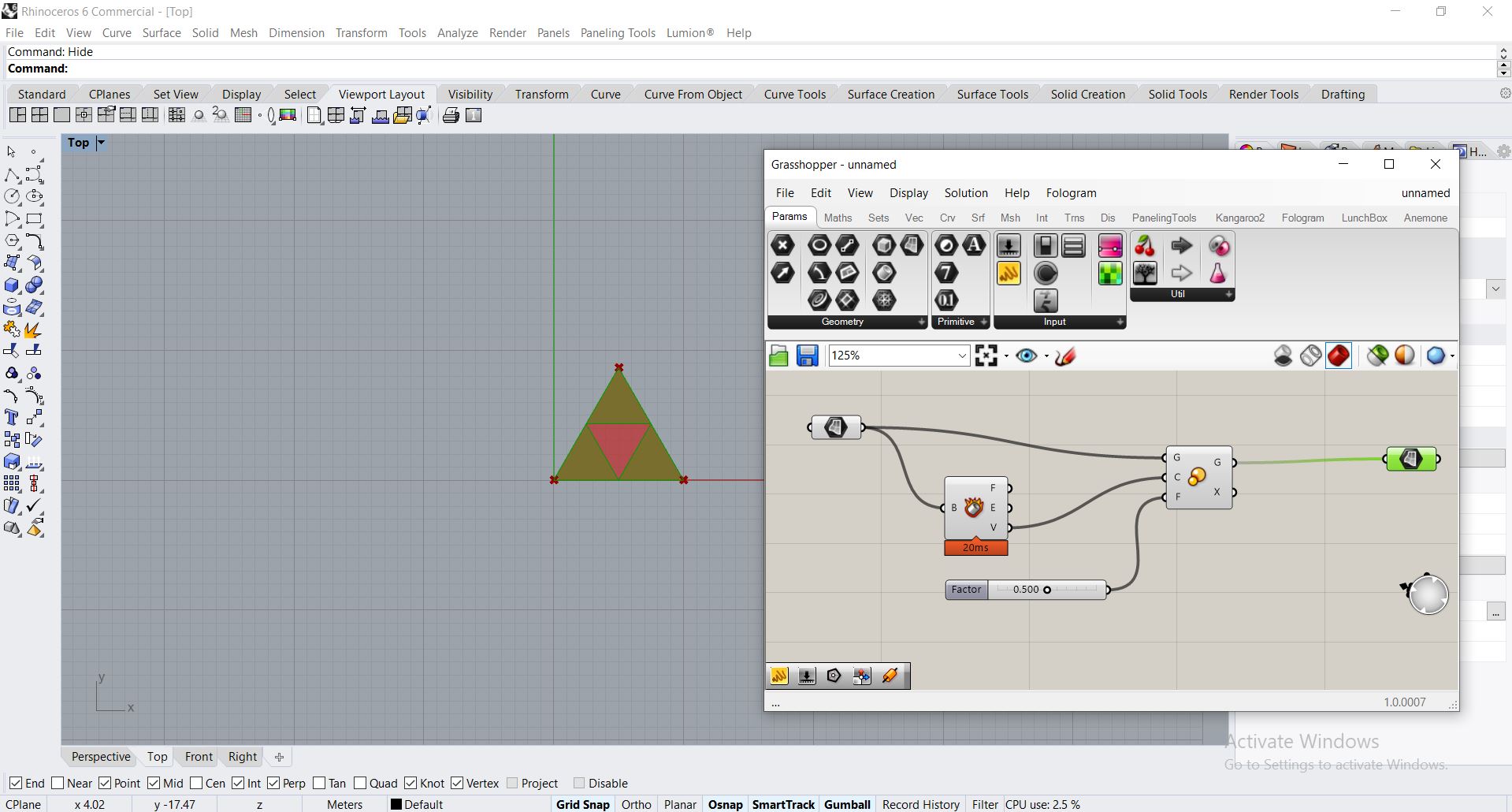
• Construire le mécanisme récursif

Exactement comme dans le cours précédent

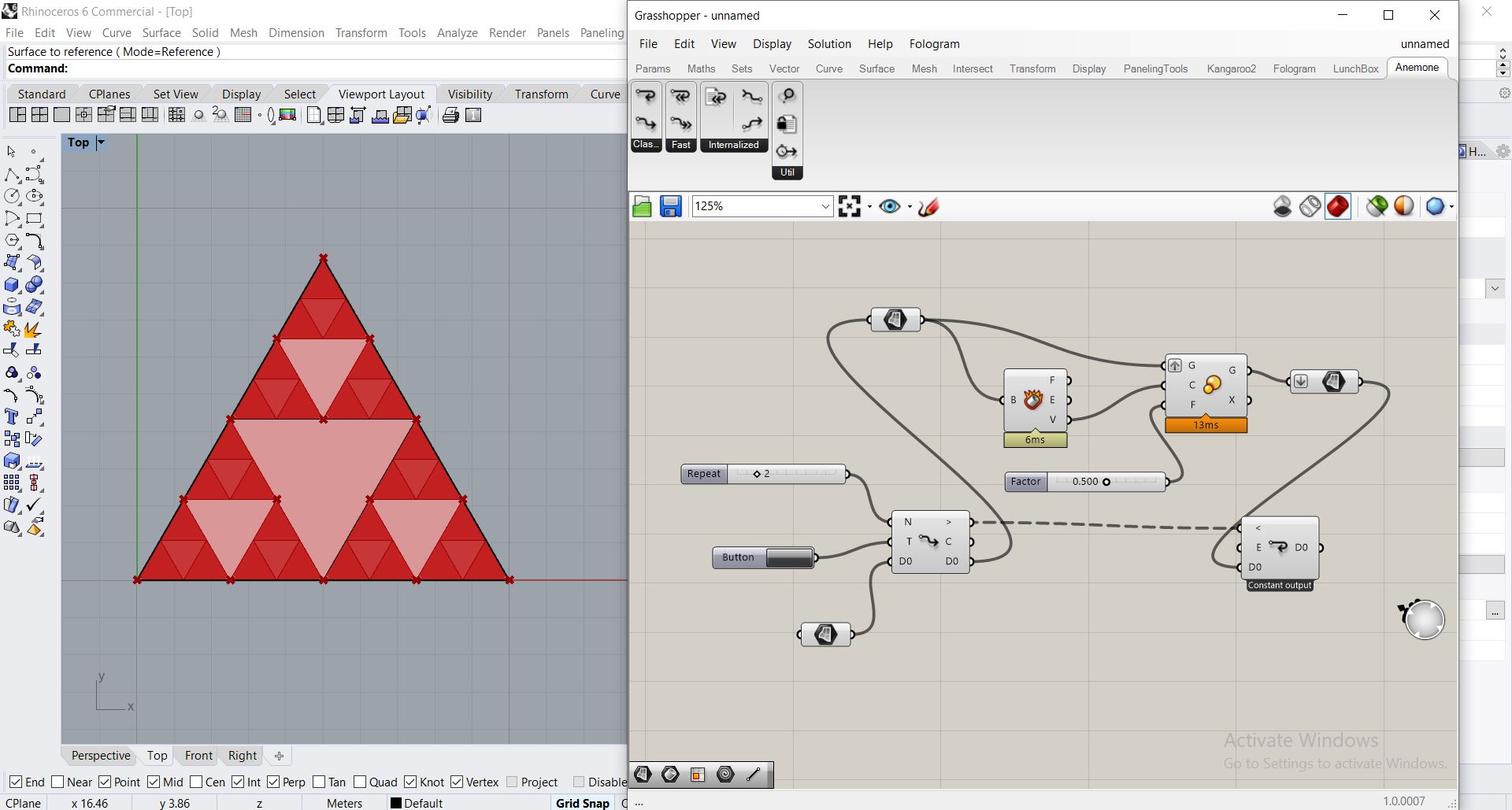
(Je n’arrive toujours pas à bien assimiler la fonction de graft et de flatten, et comment prevoir leur nécessité)

 

 

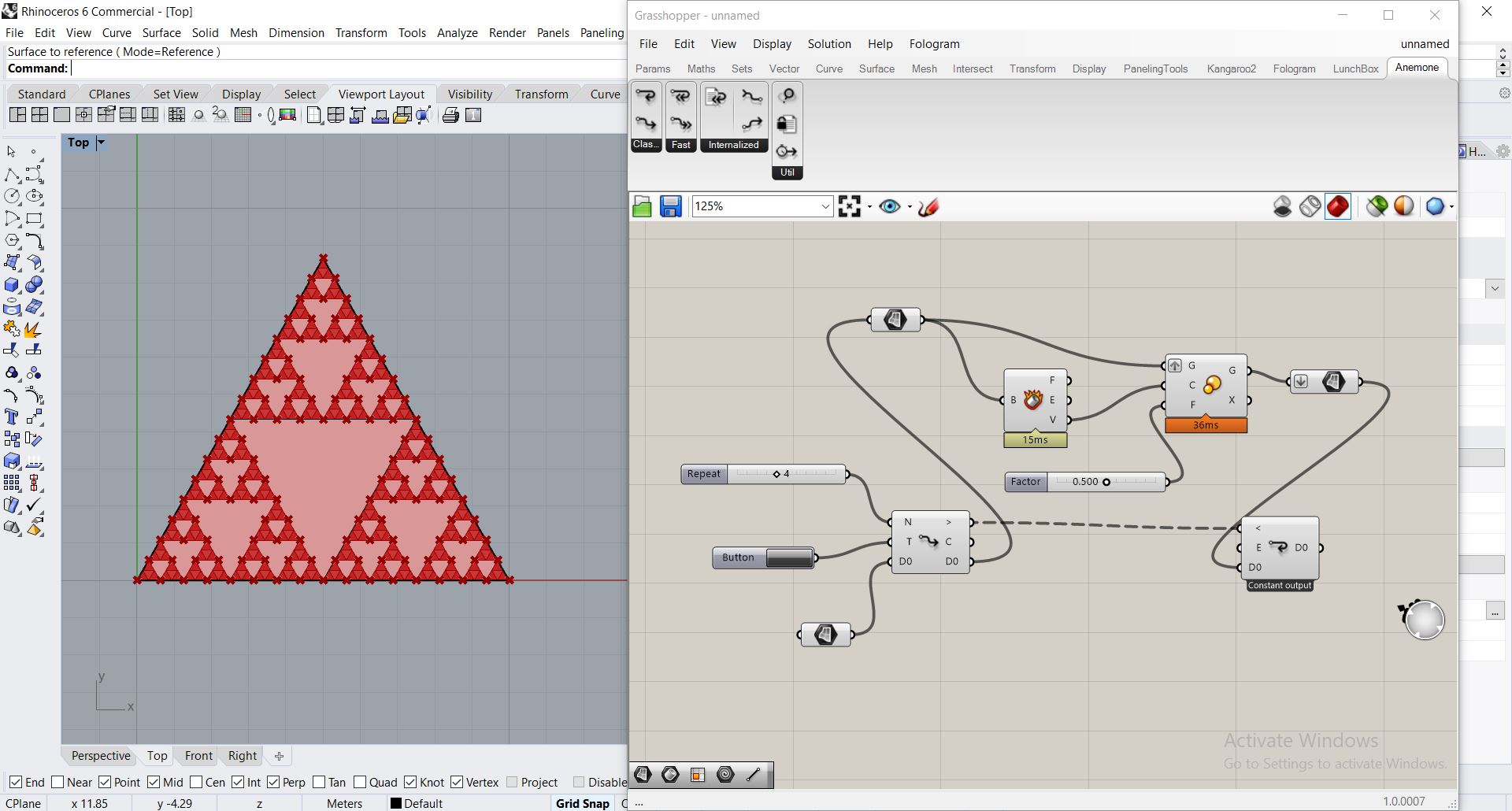
Application sur d’autres polygones reguliers

Ici la creation du polygone se fera parametriquement suivant le code suivant

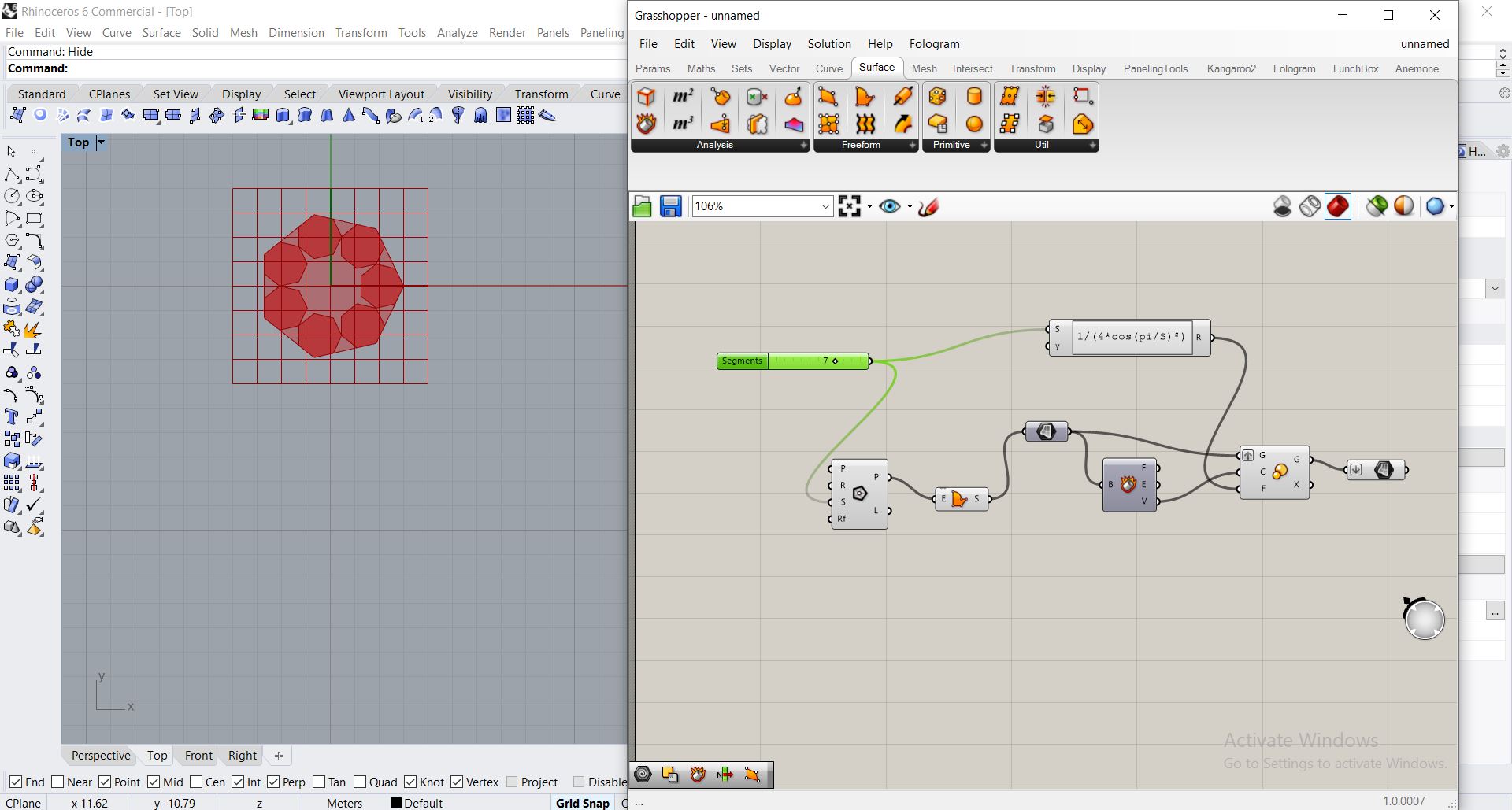
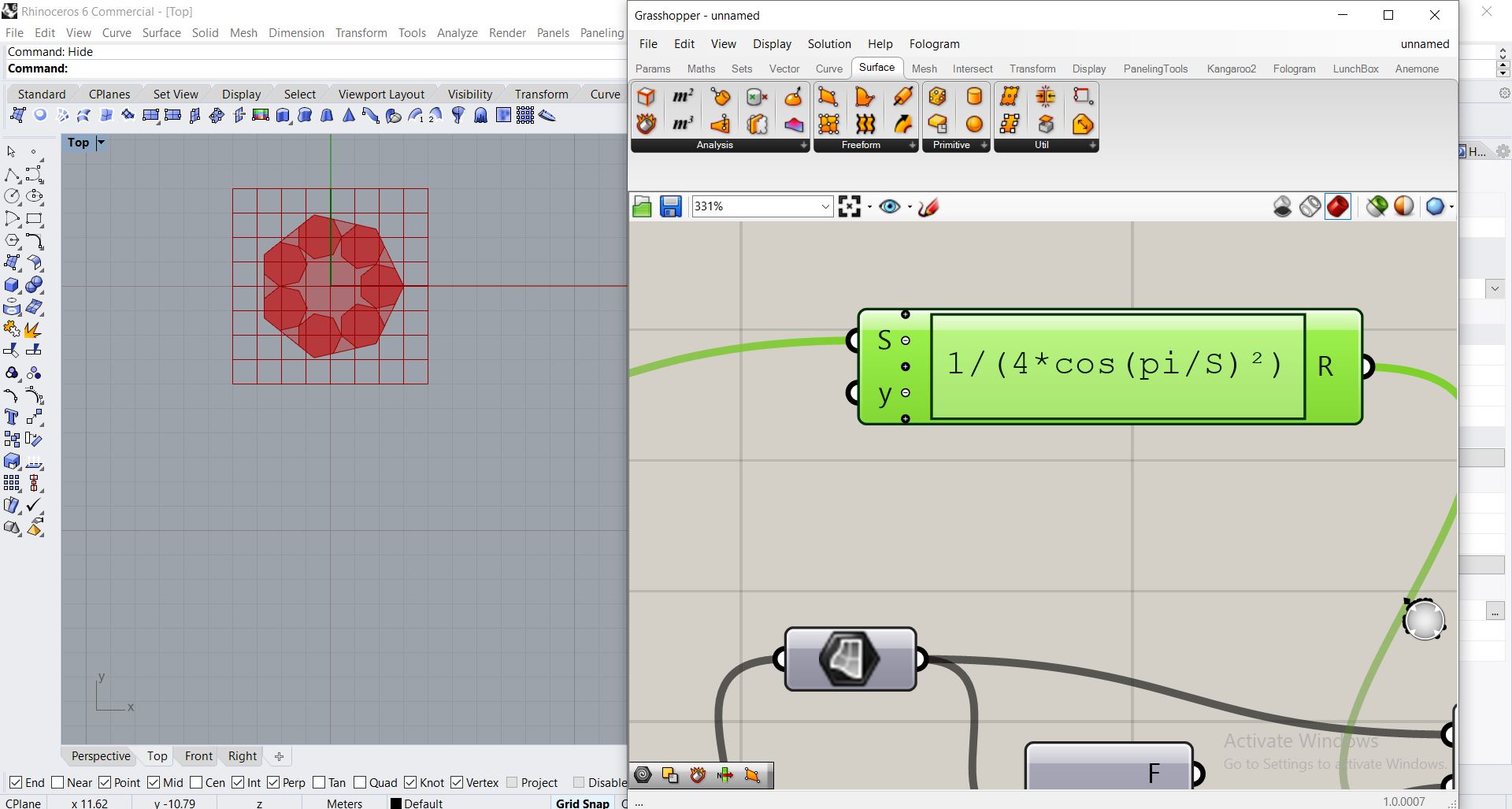
Le facteur d’homothetie suivant permet d’avoir nos geometries egalement distribuées avec un somment de contact unique (1 point), cette formule est aussi en fonction du nombre de segment du polygone (j’ai eu la curiosité de chercher la demonstration de cette formule, mais je n’ai pas réussi à la trouver)

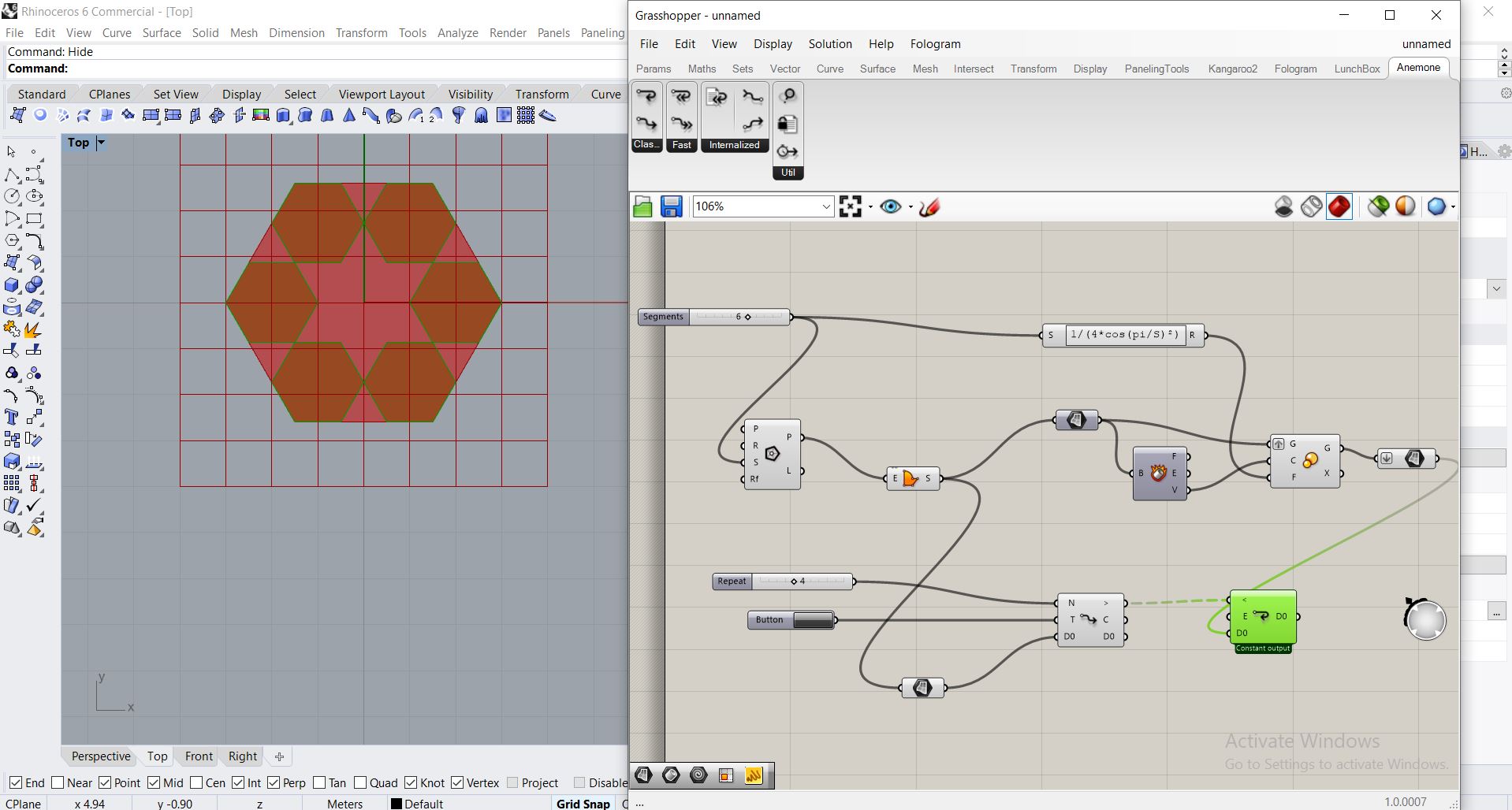
Après avoir completer le code pour activer une « loop », je n’arrive pas au résultat attendu (je n’arrive non plus à detecter le probleme)

 

Application à des objets 3D

Exemple: le cube de Sierpinsky

Il s’agit de travailler sur des solides, donc sur des Brep au depart et non d’un surface.

Le cube à 8 sommets, donc 8 homotheties à ses sommets, ayant 1/3 comme facteur, une autr homothetie de facteur 1/3 mais de centre « le milieur des segments » vient remplir les vides.

Voici le résultat obtenu

 

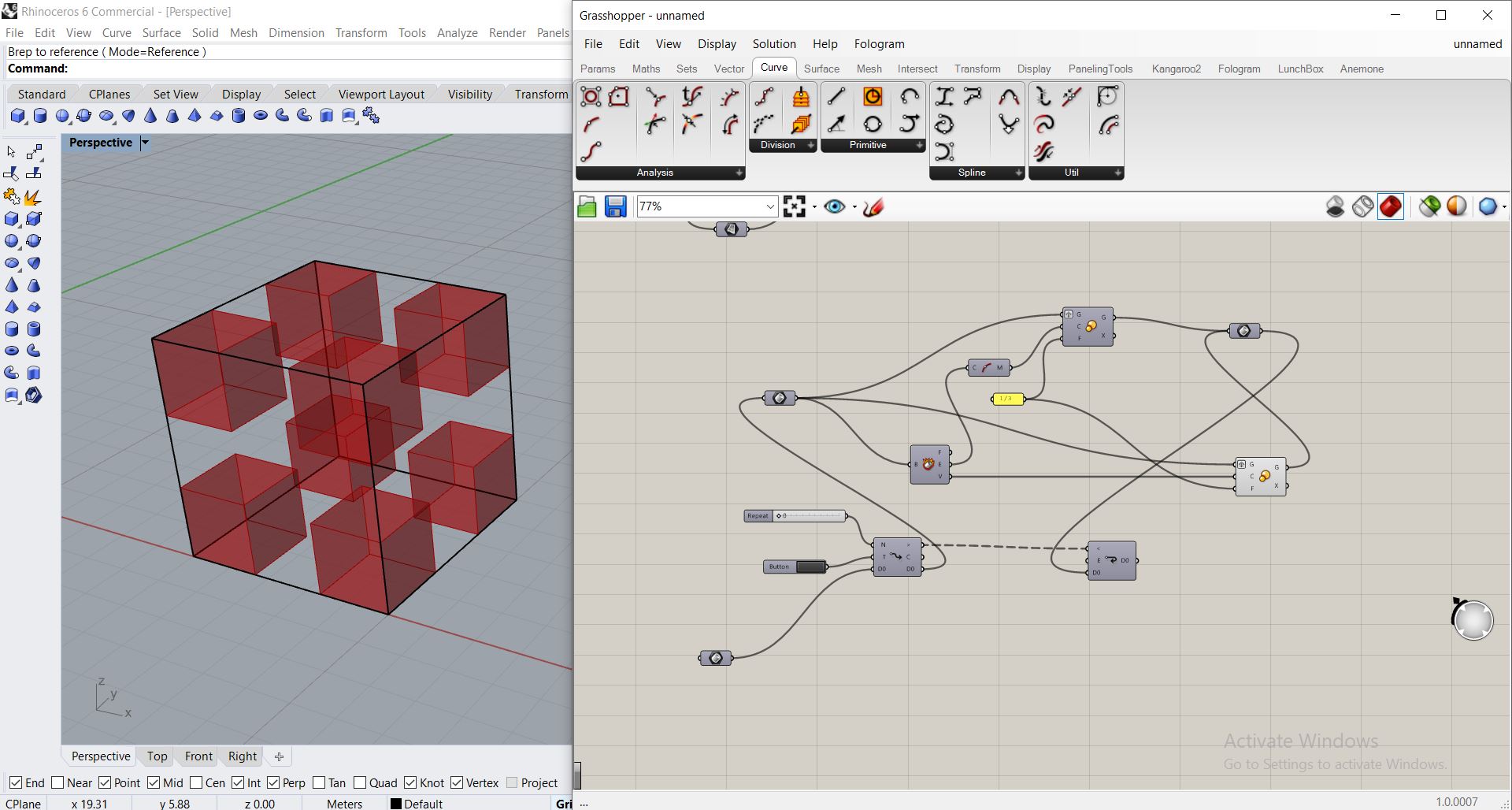
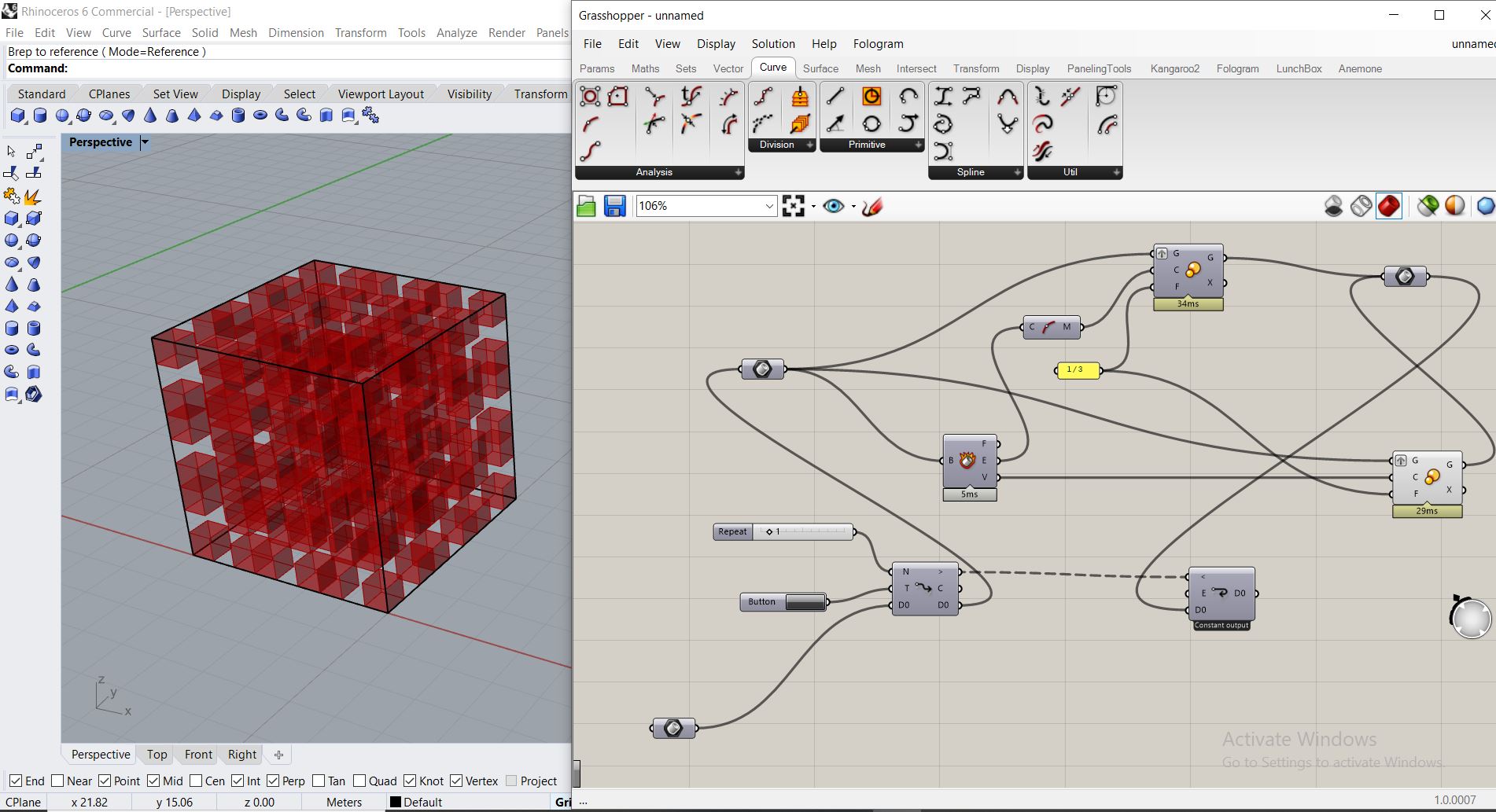
Application à l’architecture

mécanisme fractal inspiré de la conception de la façade du  Federation Square Building à Melbourne (Lab Architects – www.labarchitecture.com).

Le principe consiste à découper un triangle rectangle en 5 triangles rectangles à partir d’une règle unique appliquée récursivement. Pour aboutir à ce resultat, il fallait bien choisir les points, c’est pour cela le code pthon etait essentiel pour franchir cette etape. Après, c’etait tres interessant de voir l’application avec des transformations differentes que l’homothetie et les rotations.

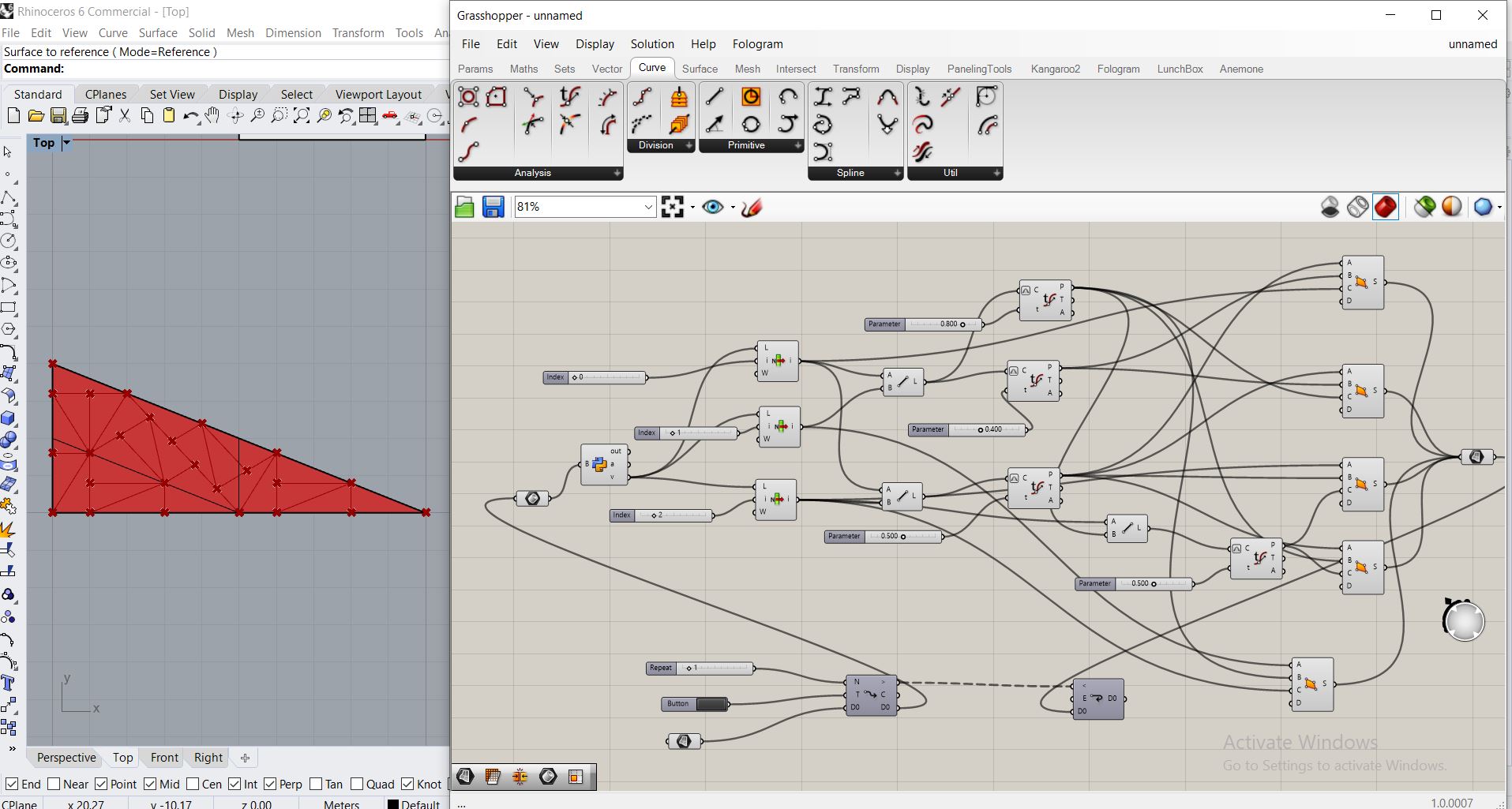
La courbe de Koch

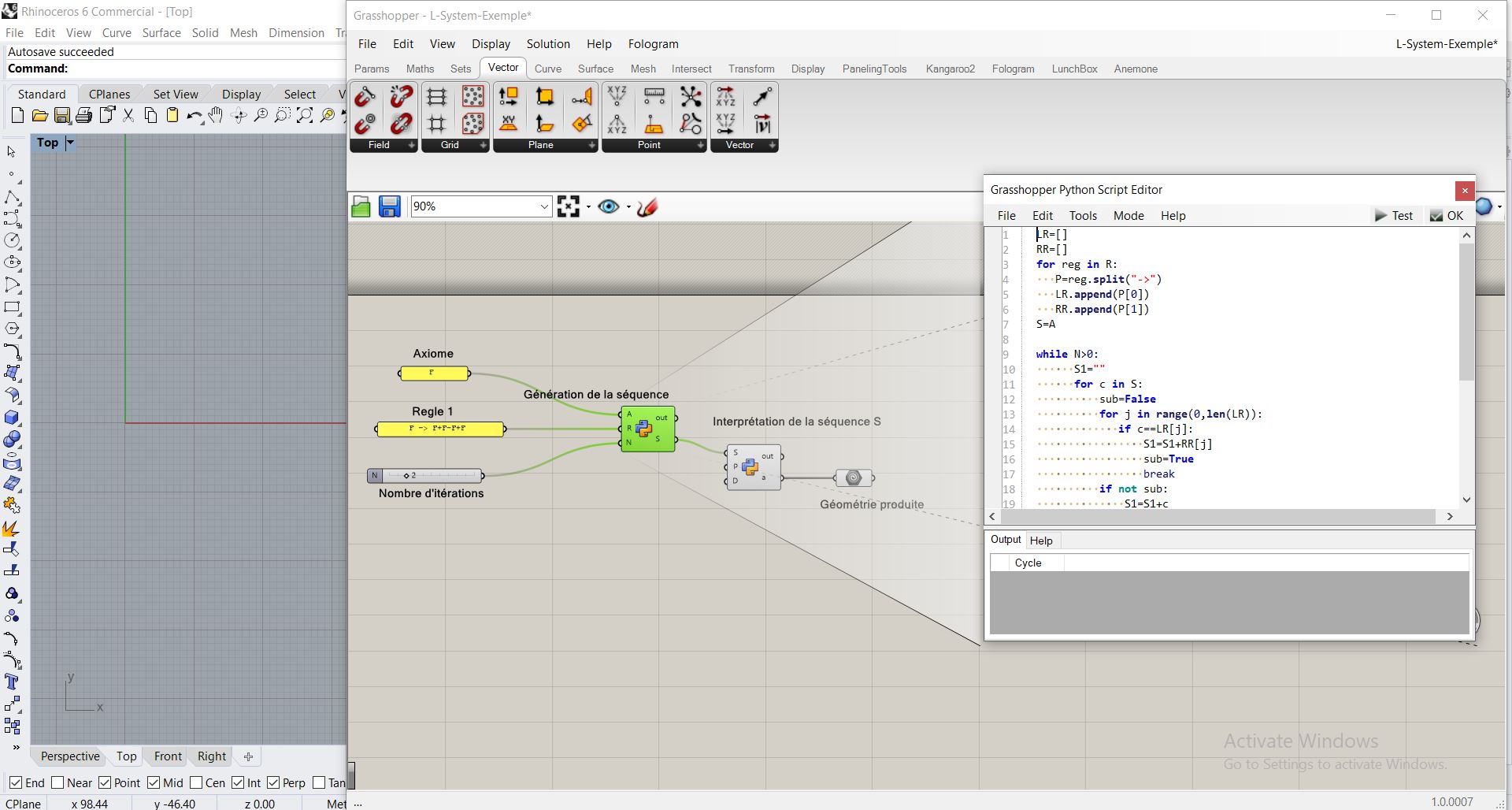
Soit le L-System suivant qui génère un objet fractal bien connue: la courbe de Koch.

Symboles et leurs interprétations:

F : Déplacer la tortue sur une longueur de 1 unité
+ : Tourne la tortue d’un angle de 60°
– : Tourne la tortue d’un angle de -60°
L’axiome : F

Les règles de substitution :
règle 1:    F -> F+F–F+F

C’etait difficile pour moi de faire fonctionner le code… Mais l’idée en elle même est interessante, ca nous permet de reduire le code en symbole (une langue simplifiée)