Cette exercice qui se place dans la continuité du précédent m’a permis d’approfondir la recherche sur la géométrie fractale en observant quelques exemple de ces application dans le domaine de l’architecture. Il est vrai qu’avec toute ces fonctionnalité ont perd parfois le but principal pour nous etudiant en architecture qui d’utiliser ces connaissance dans le cadre de notre future profession. De ce fait je trouve interessant que ce cour nous y ramène.
Exercice 1- le triangle de sierpinsky
Cette reprise du triangle
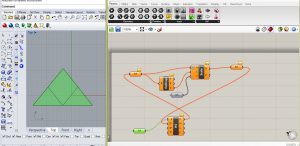
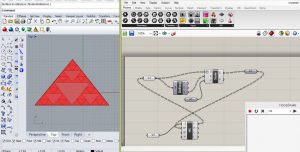
exercice 2- géométrie fractale à partir d’un polygone
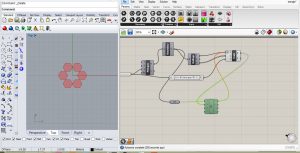
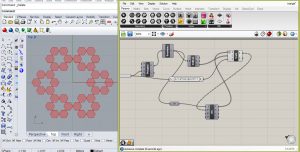
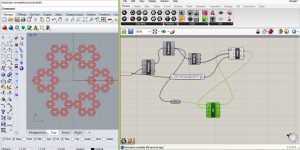
exercice 3- le cube de Sierpinsky
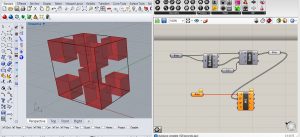
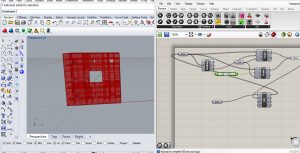
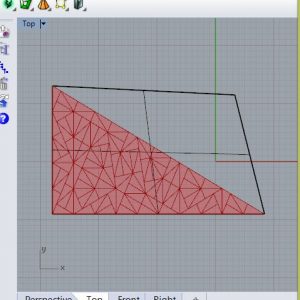
Exercice 4 – divisions successives du triangle
Après avoir réussi à installer Python, j’ai démarré cette exercice. Je n’ai rencontré qu’un problème,
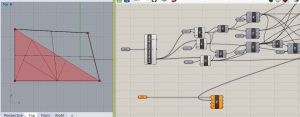
Exercice 5- Génération d’un motif en arborescence par la géométrique fractale
J’ai eu du mal trouver comment retourner les deux lignes créées par homothétie à partir de la ligne de départ. Je me suis renseigné sur le cour précédant mais mes essais n’étaient pas concluant. Puis j’ai essayer avec les méthode des lignes de l’exercice d’avant et ça a fonctionné.
Essai 1
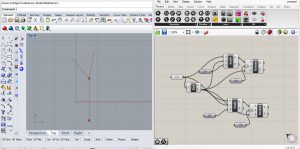
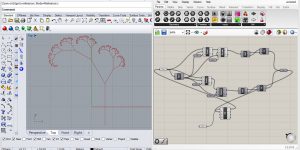
Essai 2
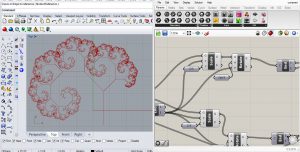
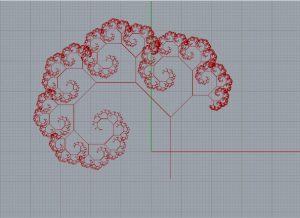
La géométrie fractale crées des motifs extrêmement plaisant à l’oeil, je me méfie cependant de son utilisation dans la création architecturale pure car il me semble que les dimensionnement des espaces ne doivent pas dépendre de la seule règle mathématique. Cependant leur utilité dans la création de façade est indéniable, les fractales créent des motifs dynamique mais qui ont également de la profondeur.
