Rendu 02 – Modélisation paramétrique et champs de force

Cours 2 – 

Ayant déjà travaillé sur grasshopper le semestre dernier, je n’ai pas rencontré de difficulté particulière à suivre le cours de cette semaine. Les étapes se sont enchaînées avec facilité, et je n’ai eu besoin de regarder les vidéos qu’au moment de rajouter un deuxième point de force, car je n’étais pas certaine de s’il fallait refaire tout le schéma ou simplement la partie du point de charge.

La création de la grille hexagonale via grasshopper était nouveau pour moi : on utilise le composant Hexagonal dans Vector/Grid, et on ajoute des sliders pour contrôler la taille de la grille. J’ai choisi de réaliser une trame carrée et ai donc utilisé le même slider pour la dimension de la grille en x et pour celle en y.

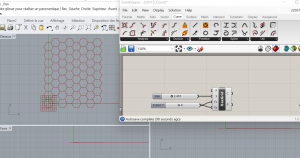
Etape 1 : Création de la grille carrée d’hexagones

La deuxième étape est celle de récupérer les sommets de tous les hexagones. On utilise à cette fin le composant Explode.

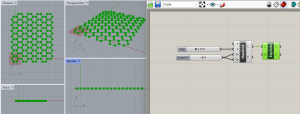
Etape 2 : Récupération de tous les sommets des hexagones

Par la suite, on créé un point qui agira comme le point de charge à l’origine des déformations de la grille. Pour cela, on créé un point directement dans rhinoceros et on utilise le composant Point de grasshopper pour l’attribuer. Dans Vector/Fields, on sélectionne le composant PointCharge qui permet de donner des attributs de force au point créé dans grasshopper. Deux Sliders permettent de donner une valeur à la déformation créée par ce point.

On créé les nouveaux hexagones issus de cette déformation grâce au composant Polyline (Curve/Spline) qui relie les nouveaux sommets entre eux.

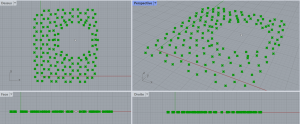
Etape 3 : Création de la nouvelle grille d’hexagones qui prend en compte la déformation créée par le point de charge

L’étape suivante a été d’ajouter un deuxième point de charge. Comme dit plus tôt, je n’avais pas compris qu’il ne fallait répéter qu’une partie du programme mais en regardant la vidéo, j’ai vu que je n’avais pas besoin de tout refaire.

Dans le menu Vector/Fileds, on sélectionne le composant Merge qui permet de cumuler les forces de plusieurs charges. C’est cette force cumulée qu’on utilise dans le programme précédent, en entrée du composant EvaluateField. On créé une surface de l’ensemble à partir du composant Boundary.

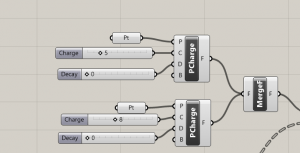
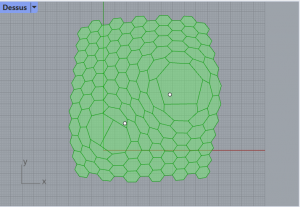
Etape 4 : Programme de grasshopper et résultat dans rhino avec l’ajout du deuxième point de charge

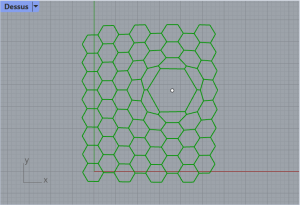
En utilisant le composant Offset (Curve/Util), on peut décaler les lignes des hexagones (en choisissant une valeur d’entrée négative, on peut les décaler vers l’intérieur et donc avoir plusieurs hexagones déformés séparés par un vide). On obtient la figure suivante :

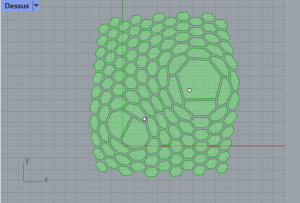
Etape 5 : Résultat final du cours

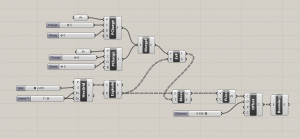
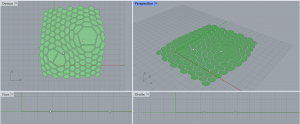
Programme grasshopper complet et vue d’ensemble du cours sur les champs de force

 

Exercice 2.1 – 

Pour la réalisation du deuxième exercice, on commence par réaliser un rectangle et une ligne dans rhino (je me suis basée sur les valeurs utilisées dans le cours).

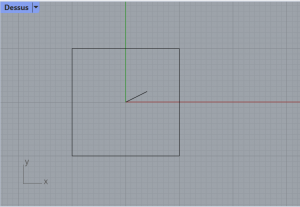
Etape 1 : Réalisation du carré et de la ligne dans Rhino

Dans grasshopper, on associe ces deux éléments à des composants Curve, puis on ajoute un composant VectorForce et un composant FieldLine. Ces composants permettent de créer à l’intérieur du carré des champs de force qui suivent l’orientation de la ligne.

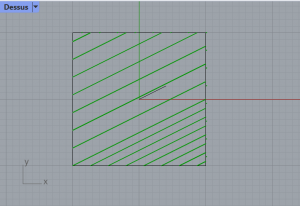
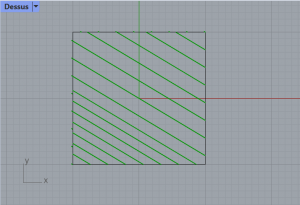
Etape 2 : Expérimentation de différentes orientations de champs de force dans le carré initial

On vient ensuite créer une force circulaire à partir des composants SpinForce et Point. 

Etape 3 : Création d’une force circulaire à l’intérieur du carré

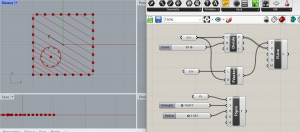
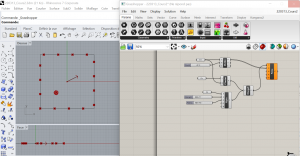
Problème : Au moment où je connecte la force issue des deux forces (en sortie de MergeForce) à l’entrée de ForceLine, mon ordinateur plante. J’ai au départ pensé que mes valeurs étaient trop importantes mais même en les diminuant, cela ne change rien au problème…

Capture d’écran prise au moment du plantage du logiciel Rhino

Solution au problème (ouf !) : En revenant sur la vidéo en détail, je me suis aperçue que j’avais oublié de connecter le rectangle à l’entrée Bounds (B) de SpinForce ! Une fois cette erreur réparée, le programme fonctionne correctement et j’arrive à avoir des champs de force modifiés par cette force circulaire.

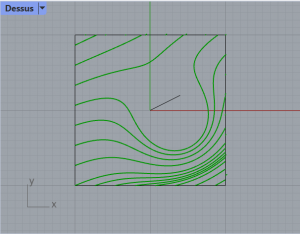
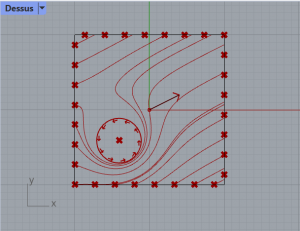
Etape 4 : Champs de force obtenus avec la déformation supplémentaire créée par le champ radial

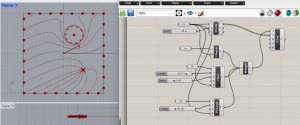
Etape 5 : Dessin final des champs de force obtenu et programme grasshopper

J’ai apprécié ce travail, bien que je ne sois pas sûre de son utilisation dans le domaine de l’architecture (permet-il de visualiser les champs de force sur une structure métallique par exemple ?). En revanche, j’ai trouvé intéressant l’utilisation d’une force négative et son impact sur les champs de force initiaux.

 

Exercice 2.2 – 

J’ai souhaité expérimenter ce même système avec la forme d’un cercle (en me basant sur les informations du site suivant : Vector Field Tools in Grasshopper – Basic + and – Point Charges – Example 7.1 | Generative Landscapes (wordpress.com)

En utilisant deux points de charges à deux extrémités d’un seul diamètre, et en faisant varier les paramètres de charge et ceux de decay, on obtient différentes figures.

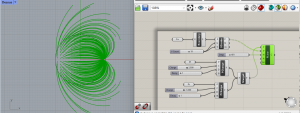
Points de charges : +2 / -1 et decay : 1

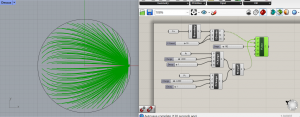
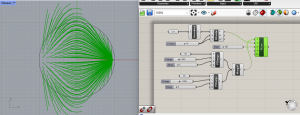
Points de charges : +1 / -4 et decay : 1

En faisant varier ces paramètres, et en variant également le nombre de points de charge, on peut obtenir différentes courbes plus ou moins à l’intérieur du cercle. J’ai trouvé difficile d’arriver à comprendre comment les courbes allaient réagir en modifiant telle ou telle valeur.

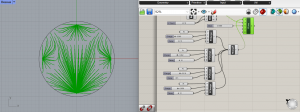
Figures finales obtenues, et programme correspondant