Exercise 4 – Simulations physiques 1

J’ai trouvé cette série d’exercices très intéressante parce qu’ils m’ont donné la possibilité de comprendre comment certaines architectures impensables ont été modélisées avec les programmes standard de modélisation 3D comme Sketchup et encore moins avec les programmes BIM comme Archicad. De plus, pour l’examen de projet, basé sur des architectures abstraites, je pensais à utiliser une de ces méthodes, même si je ne suis pas assez familier avec le programme pour l’instant, peut-être en travaillant sur un de mes projets, je peux en comprendre plus en enfonçant les opérations.

EXERCISE 1

Étape 1

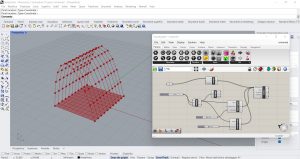
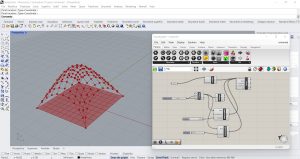
J’ai entré une Mesh Plane (Mesh/Primitive) et l’ai divisée en parts égales grâce à la commande Mesh Edge (Mesh/Analysis). Pour vérifier la hauteur et la largeur des pièces j’ai inséré un Slider compris entre 0 et 20. J’ai ensuite inséré des points dans Rhino liés au paramètre Point de Grasshopper. J’ai inséré les points des deux côtés opposés du maillage en correspondance des divisions effectuées. Grâce au plug in Kangaroo, je vais entrer le paramètre Solver (Kangaroo/Main) qui va calculer ma structure. J’insère ensuite le paramètre Anchor (Kangaroo/GoalsPt) pour maintenir les points insérés dans Rhino comme des pases de la structure. Je connecte les points que j’ai placés dans Rhino avec la commande Point à l’entrée P du paramètre Anchor. Et la sortie du paramètre Anchor à l’entrée Goal object du paramètre Solver. J’insère ensuite une Edge Lenghts (Kangaroo/Goals Mesh) et connecte le maillage créé dans Rhino à l’entrée M du paramètre Edge Lenghts. Ensuite, je connecte la sortie du paramètre Edge Lenghts à l’entrée Goal object du paramètre Solver. J’applique ensuite une force aux points du Mesh grâce au paramètre Vertex Load (Kangaroo/Goals Mesh) que je connecte à la Mesh créée sur Rhino. Je mets un curseur pour régler la force des points et un pour régler la tension entre les points. Je connecte le Vertex Load à l’entrée Goal object du Solver. J’ai ensuite ajouté d’autres points dans Rhino pour obtenir une structure à 4 arcs.

EXERCISE 2

Étape 1

Je dessine un contour polygonal de forme non carrée sur Rhino. J’associe cette polyligne au paramètre Curve (Params/Geometry) de Grasshopper pour la modifier paramétriquement. Transformez ce contour en surface avec le paramètre Boundary Surface (Surface/Freeform), puis transformez la surface en maillage avec la commande Mesh Brep (Mesh/Util). Je divise le maillage avec le paramètre Mesh Edges (Mesh/Analysis). En utilisant la commande Settings Custom (Mesh/Util), nous pouvons modifier les paramètres de division du maillage. Je mets des Sliders pour varier ce type de paramètres. J’applique des forces physiques sur ce maillage de base grâce au plug in Kangaroo. J’insère un Solver et des points d’ancrage grâce à la commande Anchor. Comme points d’ancrage, j’utilise la commande Naked Vertices (Kangaroo/Mesh) qui me permet de sélectionner tous les points sur le contour extérieur du maillage. Je connecte son entrée à la Mesh et l’utilise sortie Naked Point à l’entrée P du paramètre Anchor pour sélectionner ces points comme points d’ancrage de la structure. J’entre le paramètre qui génère des tensions sur le maillage appelé Edges Lenghts (Kangaroo/Goals Mesh) et je le connecte au maillage de départ. J’insère également le paramètre Vertex Load pour donner de la force aux points. Je règle l’intensité des deux forces grâce à des curseurs. Je connecte enfin les deux forces créées et les points d’ancrage au Solver.

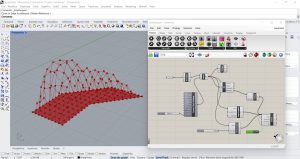
Étape 2

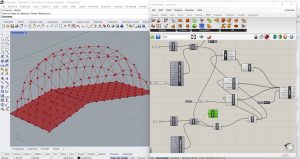
Quand les formes sont complexes, je peux décomposer le maillage en formes plus simples. J’ai donc divisé la forme de départ en deux formes plus simples, j’ai créé pour chacune des deux courbes la surface, le maillage et la division du maillage avec la possibilité de modifier les paramètres de ces divisions. Je suis donc les mêmes étapes que celles que j’ai vues en premier, mais pour les deux courbes. Je fusionne ensuite les maillages avec le paramètre Mesh Joint (Mesh/Util). Je connecte les deux maillages pour les relier. Je connecte les deux maillages reliés, puis la sortie du Mesh Joint aux commandes Anchor, Edgeslenghts et Vertexload. Pour supprimer le point de suture des deux maillages, utilisez le paramètre Weld Mesh (Mesh/Util). Je connecte enfin ce paramètre aux trois commandes connectées au Solver (Anchor, Edgeslenghts, Veterxload). J’obtiens un autre type de maillage plus régulier.

EXERCISE 3

Je crée une courbe de contour à ma surface. Je connecte la courbe de Rhino au paramètre Curve de Grasshopper, puis je crée une surface avec la commande Boundary Surface. Je crée ensuite un maillage avec la commande Mesh Brep. J’entre le paramètre Settings Custom pour modifier les paramètres du maillage. J’insère alors le paramètre Mesh Edges pour diviser mon maillage. Je dois créer un maillage isotrope. À ce stade, j’ai eu un problème que j’avais rencontré dans l’autre exercice, je ne trouve pas dans le panneau Kangaroo – Mesh la commande Simple Remesh pour créer la surface isotrope. Je n’ai donc pas pu aller plus loin dans cet exercice. Où puis-je trouver cette commande ? Dans un autre panneau? Je m’excuse si ce doute avait déjà été éclairci lors de l’appel de mardi, mais malheureusement je suis un autre cours le mardi et je ne peux pas être présent aux appels.

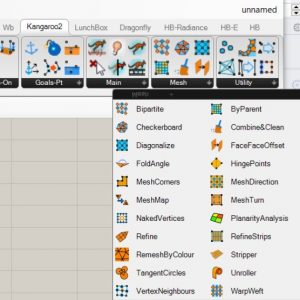
EXERCISE 4

Étape 1

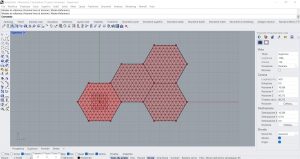
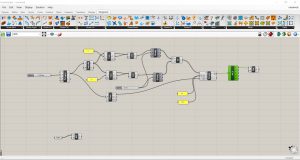
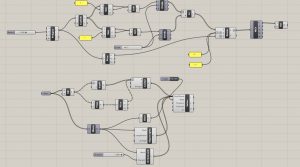
Le quatrième exercice a été un peu difficile à suivre pour les quelques indications mais j’ai quand même réussi à le compléter, notamment parce qu’il ne prévoyait pas l’utilisation de la commande Simple Remesh que je ne trouve pas. J’ai commencé par créer la forme hexagonale de départ avec la commande Polygon (Curve/Primitive) à laquelle j’ai associé un curseur pour contrôler la taille. Je devais ensuite diviser l’hexagone en triangles en utilisant des lignes inclinées pour créer ensuite le maillage. J’ai entré le paramètre Explode (Curve/Util) pour exploser le périmètre de l’hexagone. J’ai ajouté deux List Item (Sets/List) et connecté leurs entrées L (List) à la sortie S (Segment as List) du paramètre Explode. J’ai ajusté l’Index des deux paramètres grâce à l’insertion directe de deux nombres (0;3). J’ai enfin relié la sortie de ces deux paramètres à deux autres paramètres appelés Join Curves (Curve/Util). À leur tour, j’ai relié ces deux autres paramètres à deux autres nouveaux paramètres appelés Divide Curve (Curve/Division) à laquelle la sortie C (Count) j’ai connecté un curseur afin de pouvoir varier le nombre de lignes créées. J’ai enfin connecté un paramètre Divide à l’entrée A de la commande Line (Curve/Primitive) que j’ai ajouté et l’autre paramètre à l’entrée B. Nous obtenons ainsi un cadre de lignes sur lequel nous appliquerons deux doublons polaires avec un pas de 60 degrés grâce à la commande Rotation (Traform/Euclidean). Il s’agit donc de calculer toutes les intersections de ces lignes pour produire les points internes (Intersection/Physique/Courbes multiples). Enfin, vous pouvez créer le maillage en utilisant la commande Delaunay Mesh (Mesh/Triangulation).
J’ai ensuite dupliqué le maillage dans Rhino trois fois et connecté ces maillages à la commande Mesh de Grasshopper. J’y ai relié la commande Mesh Corner (Kangaroo/Mesh) pour récupérer les points de contour du maillage qui seront les points d’ancrage de la structure.

Étape 2

J’utilise aussi les centres des hexagones comme points d’ancrage en insérant deux paramètres : l’un qui calcule les contours des hexagones (Curve/Spline/Polyline) et l’autre qui calcule le centre (Curve/Analysis/Polygon Center). J’insère le composant Anchor pour définir les points d’ancrage. Comme pour les exercices précédents, j’insère les composants Edges Lenghts et Veterx Load pour créer la force aux points et la tension dans le maillage. Je connecte les trois paramètres au Solver qui génère la forme de maillage requise.

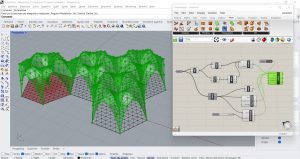
EXERCISE 5

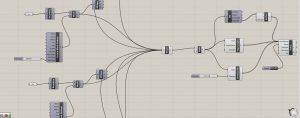
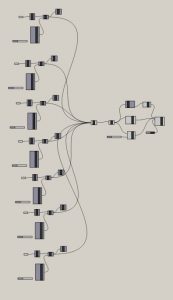
Comme dernier exercice, j’ai essayé de jouer un peu avec les formes de départ en insérant une série de triangles et en effectuant le même processus que les autres exercices. En regardant la forme initiale, je suis venu à l’esprit que vous pouvez utiliser cette technique non seulement pour la construction de l’architecture mais aussi pour la modélisation des éléments naturels. Mais je me demandais si la seule façon de créer une surface isotrope qui relierait le maillage, et qui serait donc visible sur un programme 3D ou de rendu comme Lumion, serait en utilisant la commande Simple Remesh de Kangaroo que je ne trouve pas encore.