Le triangle de Sierpinsky
Je construis une surface triangulaire sur Rhino.
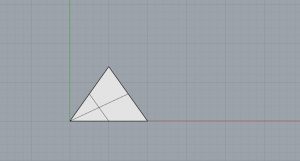
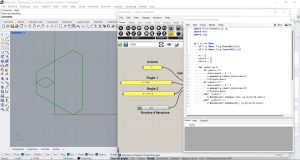
J’ai inséré un paramètre Surface (Params/Geometry) lié à la surface triangulaire nouvellement construite.Grâce au composant Deconstruction Brep (Surface/Analysis), j’analyse la surface et retourne ses sommets. Depuis ses sommets, j’applique trois homothéités avec un rapport de 0,5 grâce au composant Scale (Transform/Affine).
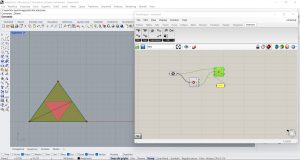
Enfin, j’ai inséré à partir du rideau Anemone les composants Loop Start et Loop End afin d’actionner le mécanisme récursif. J’ai connecté au composant Loop Start un curseur pour contrôler le nombre de répétitions, un bouton d’allumage et d’arrêt de la boucle, et j’ai défini la Surface du triangle comme modèle de référence. Après avoir vérifié que j’avais inséré le symbole Greffe sur le composant G du composant Scale, j’ai connecté les deux Boucles entre elles et la sortie Data du composant Loop Start à l’entrée de la surface de départ.
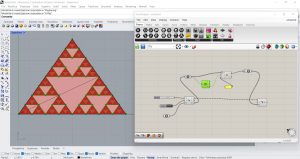
Exercices
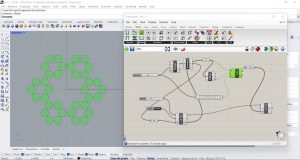
J’applique donc ce procédé à des surfaces de départ autres que le triangle. Cette fois, je ne dessine pas le triangle à la main sur Rhino, mais j’insère un curseur sur Grasshopper qui va du chiffre 5 au chiffre 8 avec des valeurs naturelles. Ce curseur me donnera le nombre de sommets de la figure que je crée directement à partir de grasshopper. Pour créer cette surface, je génère d’abord une polyligne avec le nombre de segments indiqués dans le slider grâce au composant Polygon (Curve/Primitive) puis nous transformons cette polyligne en une surface grâce au composant Boundary Surface (Surface/Freeform). J’insère comme dans l’exercice précédent un composant Surface qui prendra comme entrée la surface nouvellement créée, puis j’insère un Deconstruction Brep pour en obtenir les sommets et un composant Scale pour appliquer les homothéités. La valeur d’échelle est ajustée en joignant son entrée F à la formule « 1/(4*cos(pi/S)² » insérée grâce au composant Expression (Maths/Scripts) auquel j’ai changé la vérifiable x par le numéro du slider S et j’ai supprimé la variable y.
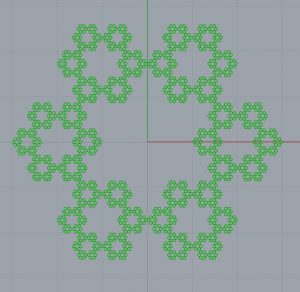
Application à des objets 3D
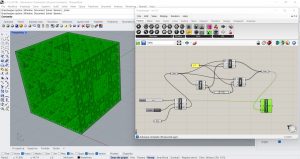
Exemple: le cube de Sierpinsky
Je suis partie du fichier du triangle de Sierpinsky auquel j’ai effacé la courbe créée dans Rhino et j’ai remplacé tous les composants Surface par 3 composants Brep (Params/Geometry). J’ai modifié le rapport d’échelle pour qu’il soit 1/3. J’ai associé l’un des trois Breps au cube que j’ai dessiné en lignes sur Rhino. J’ai donc appliqué de cette façon le processus récursif au cube et j’ai obtenu 8 répétitions homothétiques sur les 8 sommets du cube. J’ai ensuite ajouté un autre composant Scale (avec une valeur de greffe sur l’entrée G) et à son entrée G, j’ai connecté le Brep. Je positionne un composant Point One Curve (Curve/Analysis) de manière à ce qu’il soit fixé à la valeur standard de 0.5 mi et renvoie tous les points médians de tous les segments qui composent le cube. En reliant l’entrée de ce composant à la sortie Edge du Deconstruction Brep et la sortie de ce composant à l’entrée Center du composant Scale j’obtiens que le processus récursif s’applique non seulement aux sommets du cube mais également à tous les points moyens des segments qui le composent.

Application à l’architecture
J’ai trouvé l’exemple sur la façade du bâtiment Federation Square très intéressant Quini j’ai essayé de reproduire le processus. J’ai réussi à diviser le triangle en différentes sous-surfaces triangulaires qui le composent. Mais après avoir téléchargé le composant supplémentaire appelé Hoopsnake le système me donne une erreur flottante que je ne comprends pas.
Utilisation des L-systems
La courbe de Koch
J’ai suivi toutes les instructions et j’ai modifié le langage Python et il n’a pas été compliqué d’obtenir la courbe de Koch.
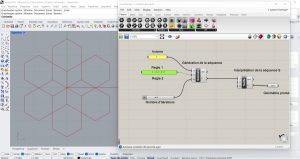
Combination of Islands and Lakes
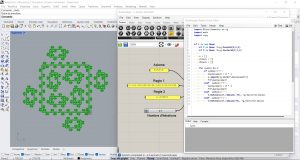
Exercices
J’ai pu faire la plupart des exercices.
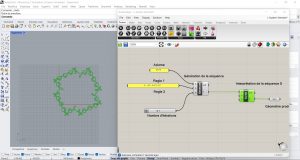
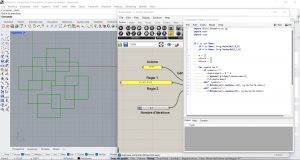

1 comment
François Guéna says:
May 18, 2022
Bon travail. Pour la façade du Federation Square Building vous pouvez essayer avec Anemone. J’ai modifié un peu le cours pour indiqué comment faire.