4 – Simulations physiques 1
Voute caténaire
Cette méthode consiste à une recherche de forme basée sur le principe de la voute caténaire, on exploite encore une fois l’application des forces mais dans une stratégie un peu différente.
Etape 1: Créer un maillaige (Mesh plane), le paramétrer (Nombre de divisions en longueur et en largeur) et choisir des points d’accroches (dans Rhino) de notre forme sur ce maillage là, dans mon exemple j’ai choisi les 4 éxtrémités de mon maillage.
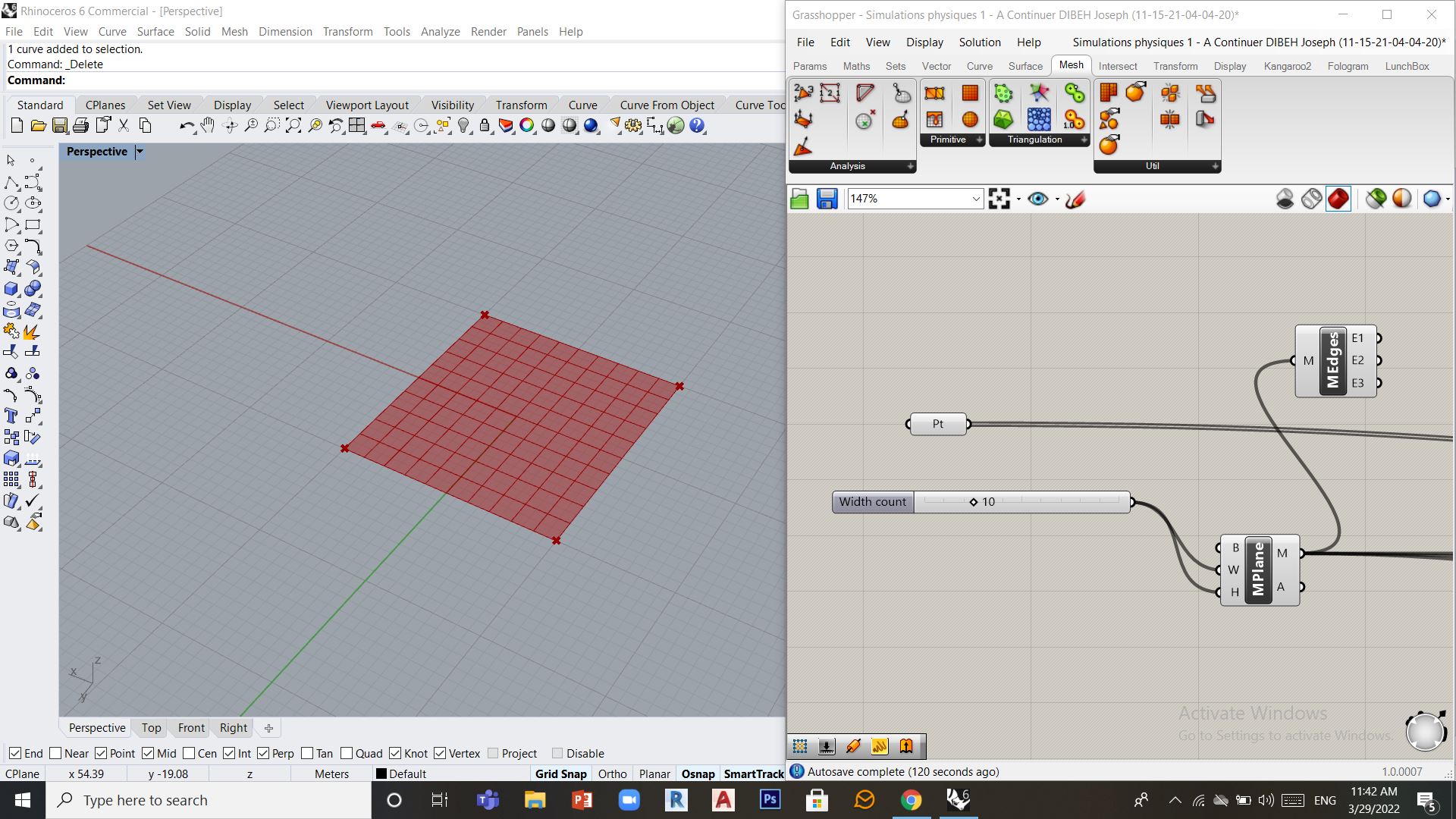
Etape 2: Ajouter des contraintes
Placer le ‘solver’ Kangaroo qui va calculer ma structure, je commence alors par définir les points d’ancrage déja dessinés sur Rhino dans l’outil (Anchor) puis on ajoute cette contrainte au solver (dans l’entrée goalobjects).
Ensuite on appeliquera des contraintes sur le maillage lui-même (l’outil EdgeLength dans la rubrique Goals-Mesh de Kangaroo)
La troisième contrainte sera d’ajouter des poids uniformes sur tout les points du maillage (VertexLoads), ces forces peuvent être paramétrer par un slider.
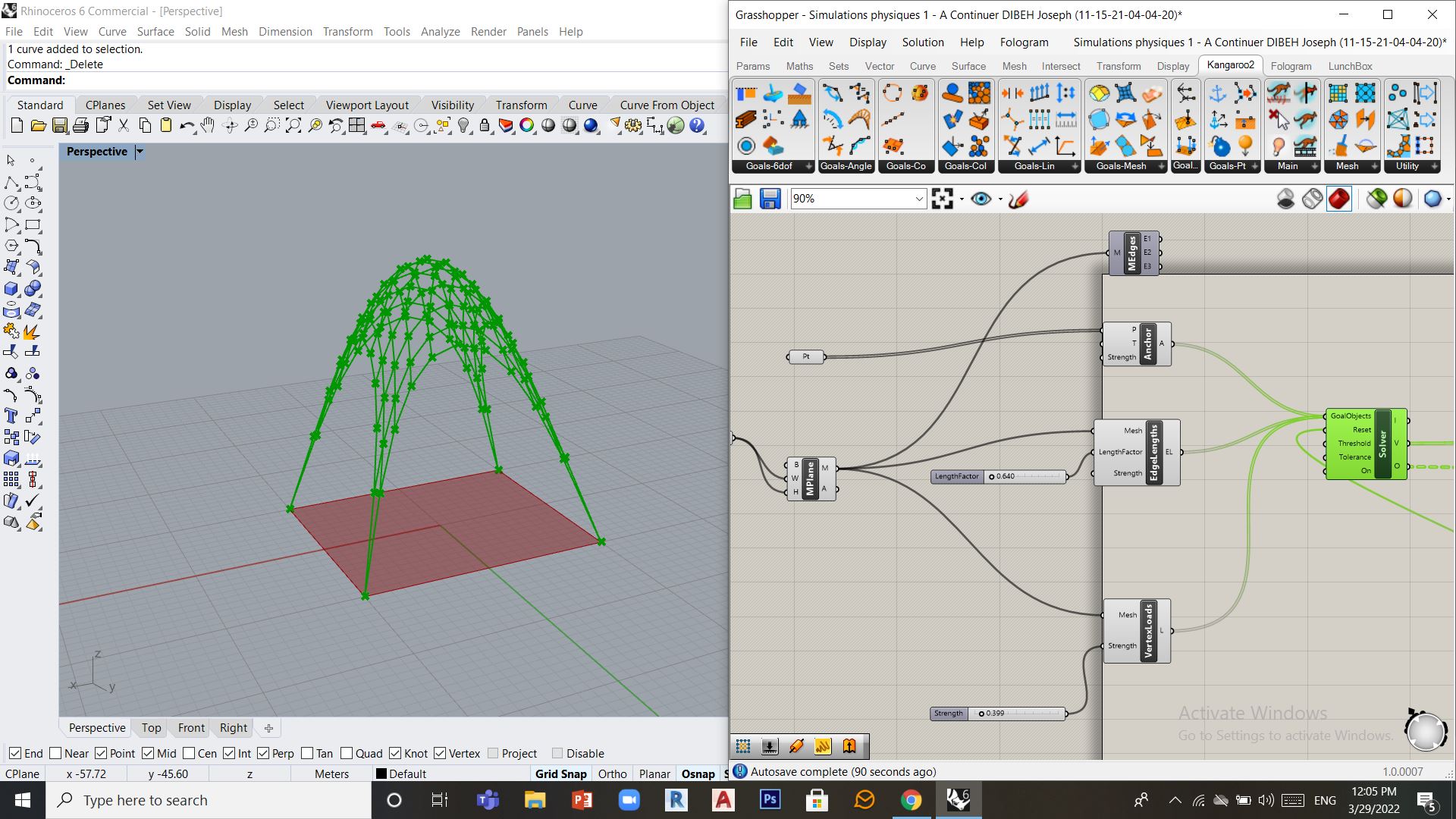
Etape 3: Contraintes additionnelles:
On peut choisir d’accrocher des points du maillage sur un plan precis, j’ai choisi par exemple d’accrocher les points de deux cotés opposés sur le plan horizontal en ajoutant une contrainte pour ces points sur l’axe des z (Outil Anchor XYZ)
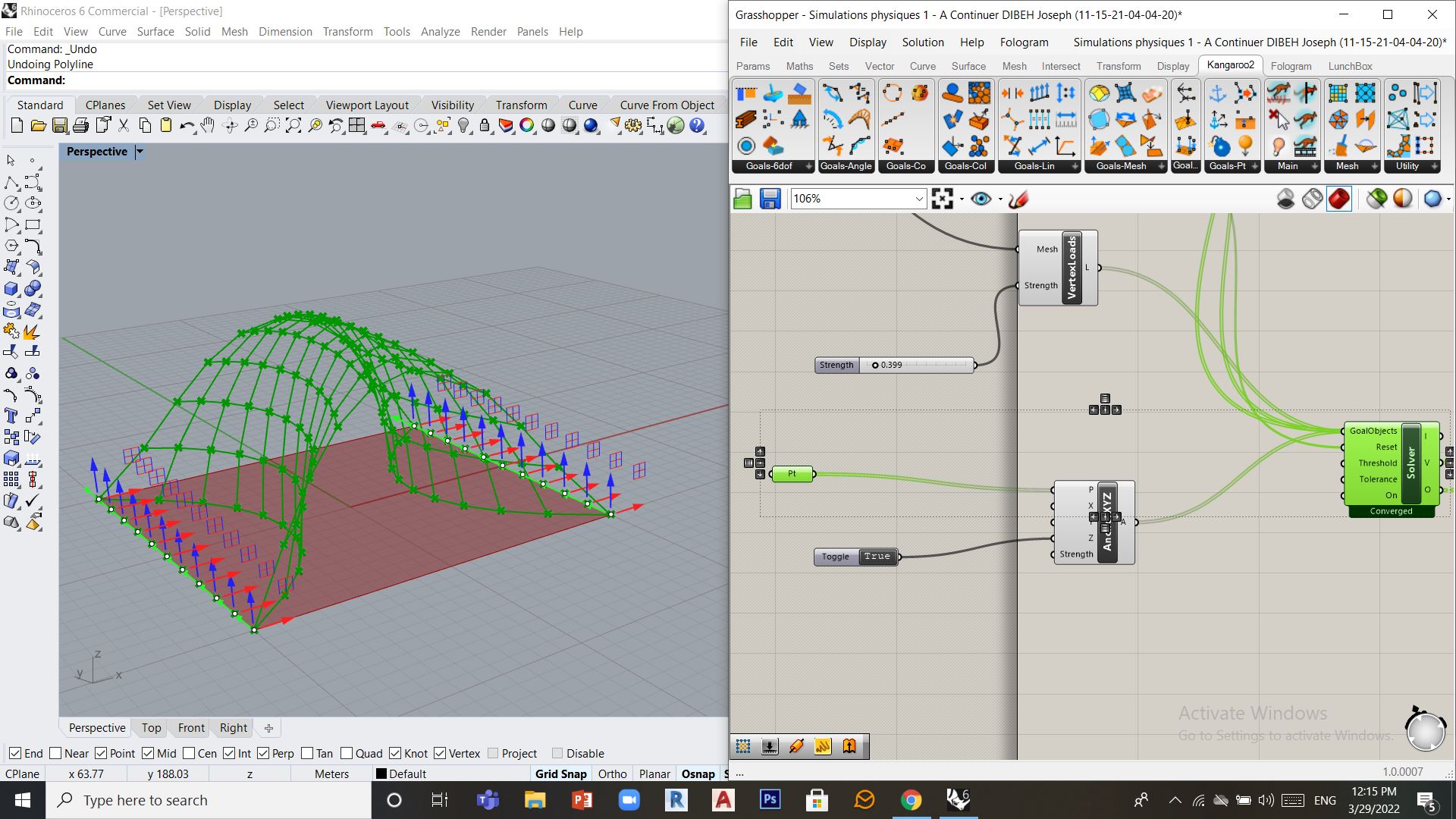
Différents types de maillages
Dans ces mécanismes de recherche de forme on part souvent d’une forme plane et la première étape consiste à la mailler. Il existe une infinité de maillages possibles pour une forme plane donnée et ce maillage aura une influence sur la forme générée . Dans les exemples précédents la forme est rectangulaire et le maillage généré est constitué de quadrangles dont on peut aisément régler le nombre dans le sens de la longueur ou de la largeur. Si la forme plane n’est pas rectangulaire le maillage généré automatiquement par les algorithmes de maillage comportera aussi des triangles voire uniquement des triangles. Par exemple le maillage de Delaunay consiste à produire un maillage triangulaire à partir de points. Les outils de maillages sont généralement paramétrables afin de produire différents résultats. On peut par exemple agir sur le type de mailles (quadrangles, triangles), sur la longueur des arêtes etc.
Etape 1: Partir sur un maillage de forme quelconque
Dans ce premier cas on va partir sur une forme polygonale non rectangulaire, on commence par dessiner ce polygone sur Rhino, on definit ce maillage sur Grasshopper (outil curve) , on crée une surface à l’intérieur (Boundary Surfaces) qu’on transforme juste après en maillage (Mesh Brep) qu’on pourra visualiser grace à l’outil (Mesh Edges)
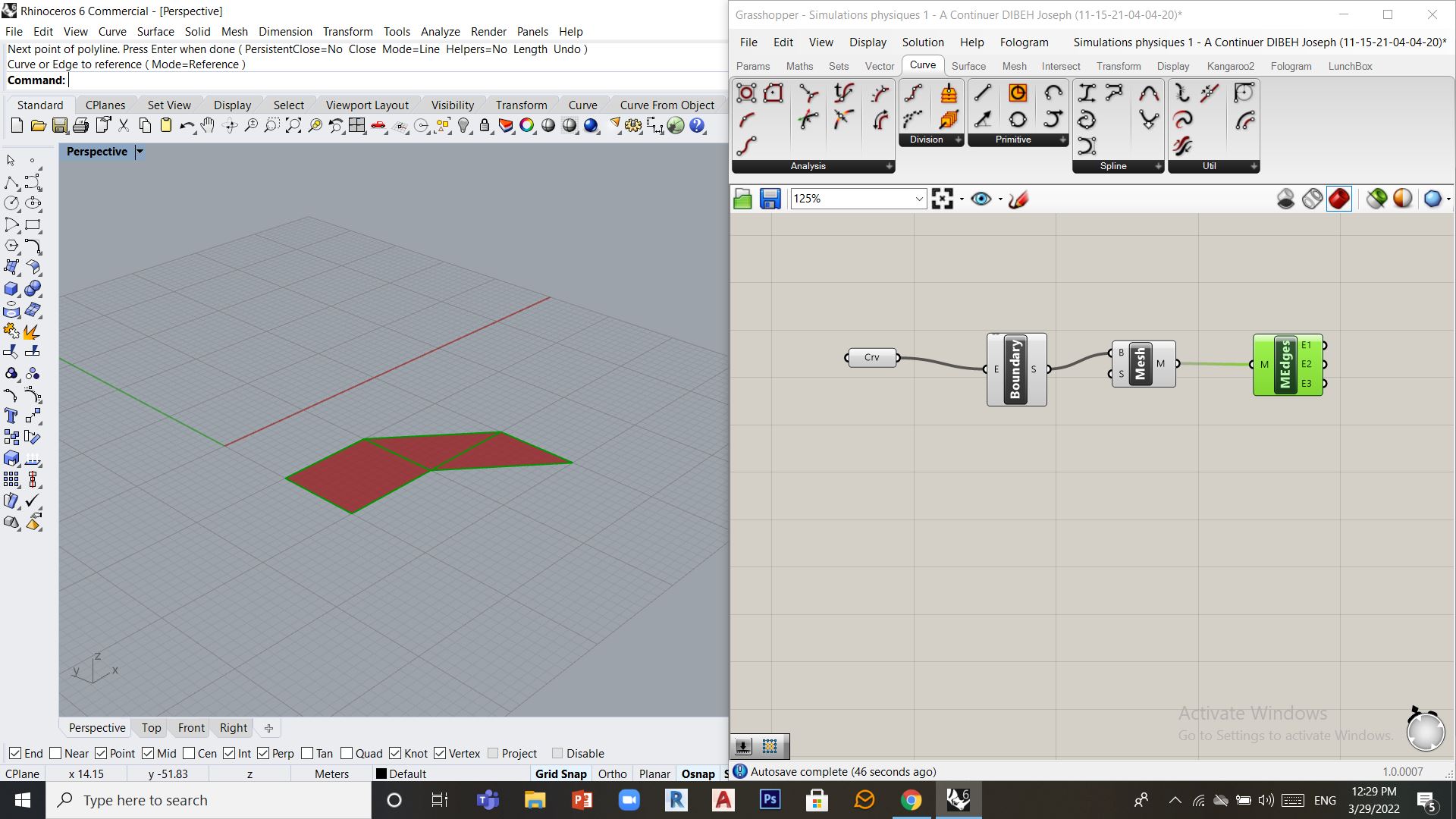
Etape 2: Parametrer le maillage
On peut ensuite paramétrer l’algorithme du maillage grace à l’outil Custom Mesh Settings qu’on insère dans l’entrée settings de l’outil Mesh Brep. On peut alors definir les extremums du nombre de quadrangle ainsi que les longueurs extremums des arrêtes de ces derniers.
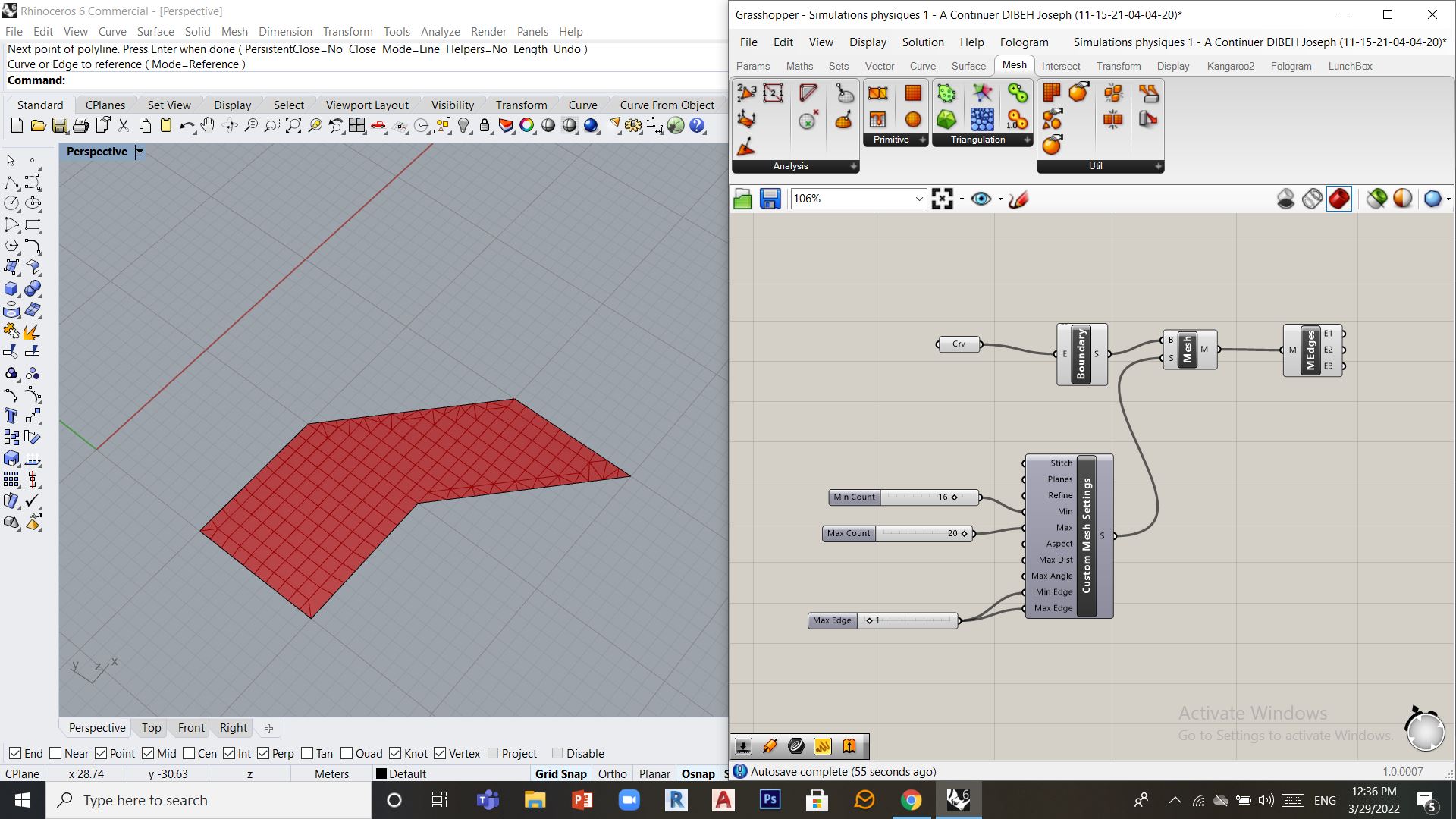
Etape 3: Solver Kangaroo
Ici c’est un peu la même procédure que l’exemple précédent, mais pour choisir les points d’ancrage, au lieu de les selectionner 1 à 1, on peut utiliser un outil intéressant de Grasshopper (NakedVertices) qui consiste à saisir les point nus d’un maillaige (or les points extérieurs)
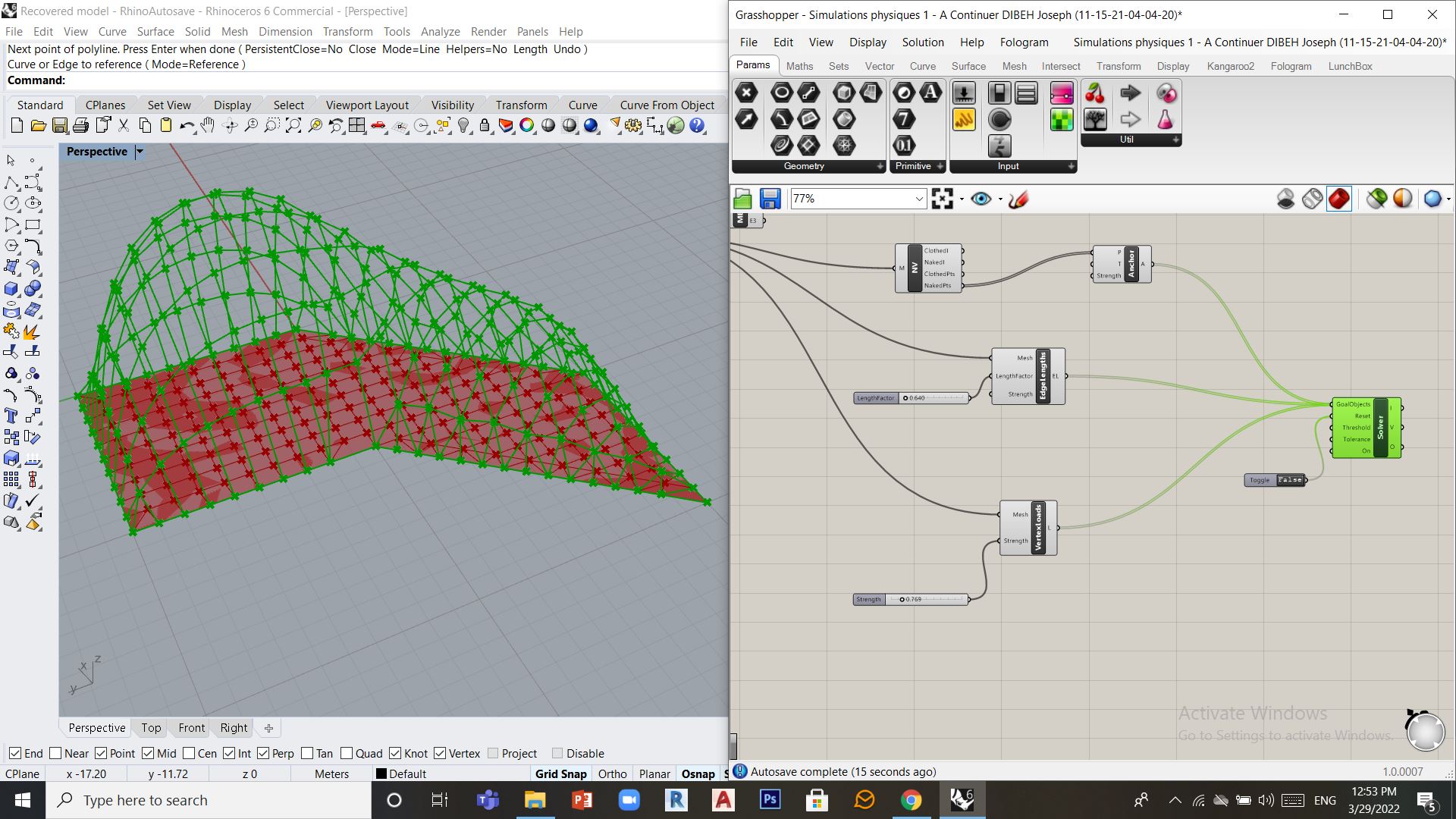
Astuce: Forme plus uniforme
Une autre approche sera de diviser le polygone en 2 quadrilataires, les transformer en maillage puis pratiquer une addition de maillage (Join Mesh), l’astuce ici sera de bien s’assuree que les maillages se joignent correctement sur les cotés communes. après avoir joint les deux maillaige on continue le travail de la même facon.
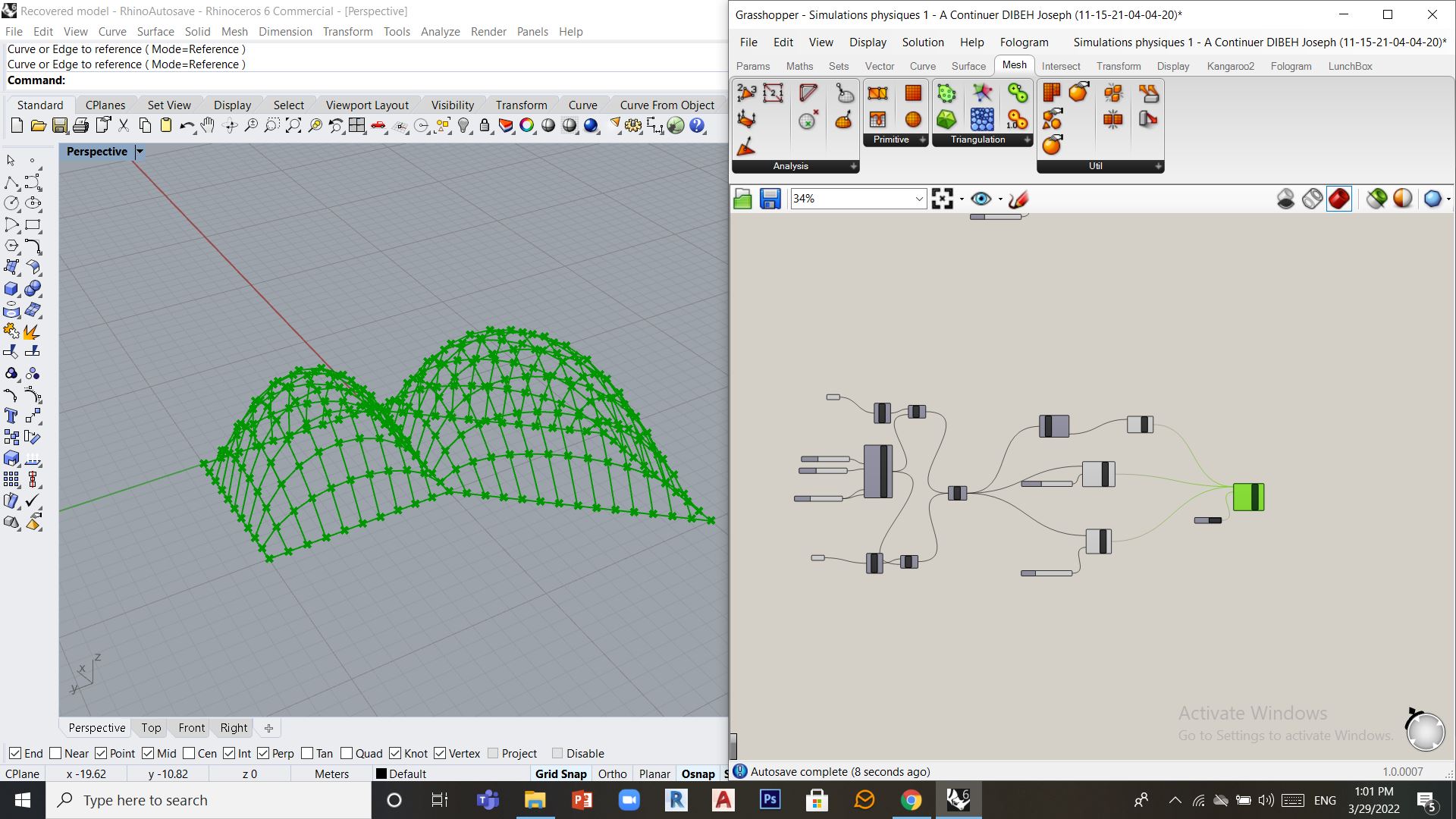
On constate tout de même qu’il existe une ligne qui divise notre maillage en deux, il faudra alors souder les points communs (les transformer en des points uniques), il faut alors passer de Join Mesh à Weld Mesh, le maillage resultant sera utiliser pour continuer le travail.
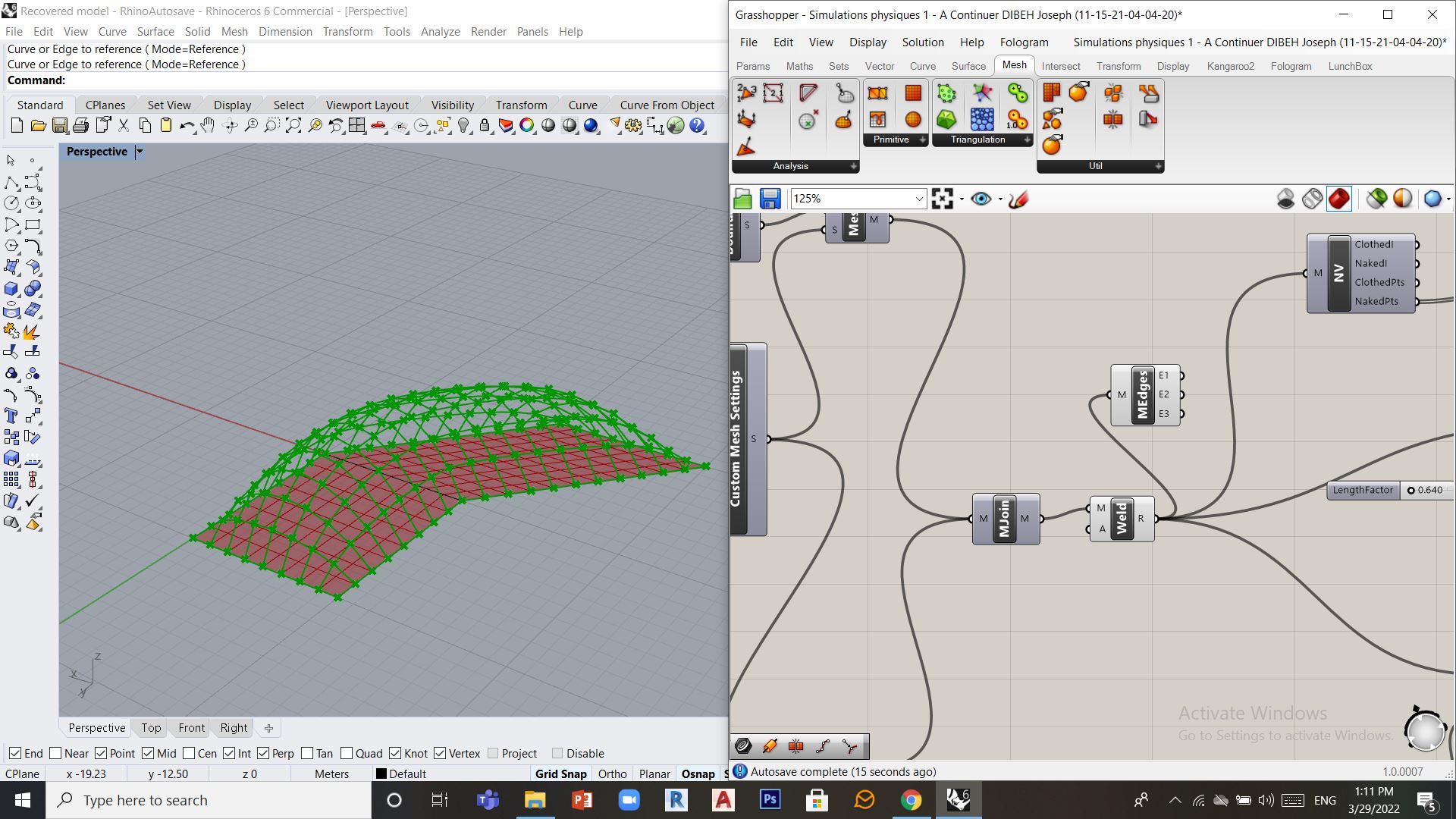
Formes complexes – Nécéssité d’un maillage isotrope
En créant un maillage en utilisant les méthodes précédentes pour des formes irrégulières on constate qu’on pourra obtenir des maillages non isotrope comme celui-là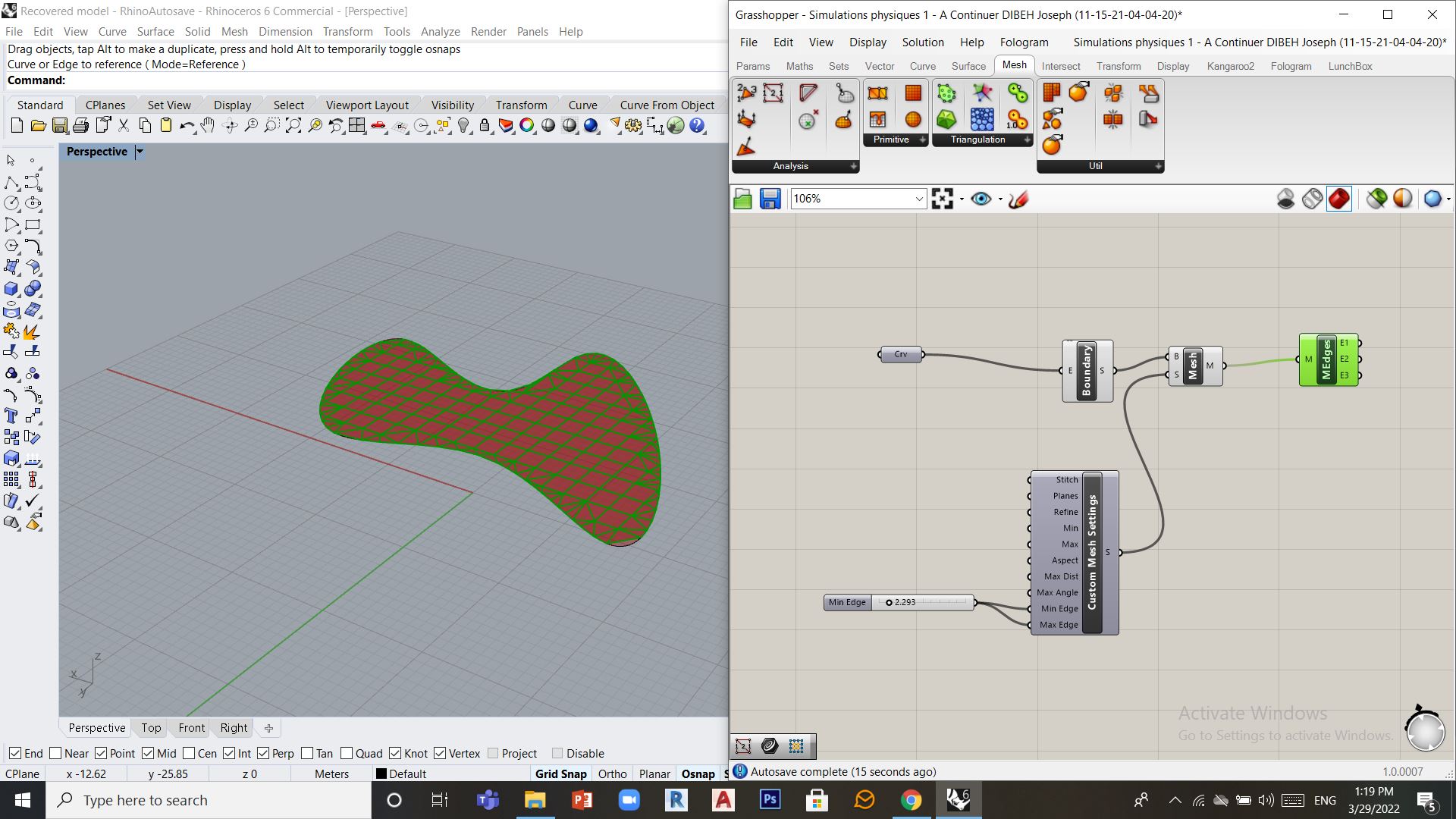
Pour créer un maillage isotrope, on peut utiliser l’outil simple ReMesh qui fera le calcul afin de produire un Maillage isotrope
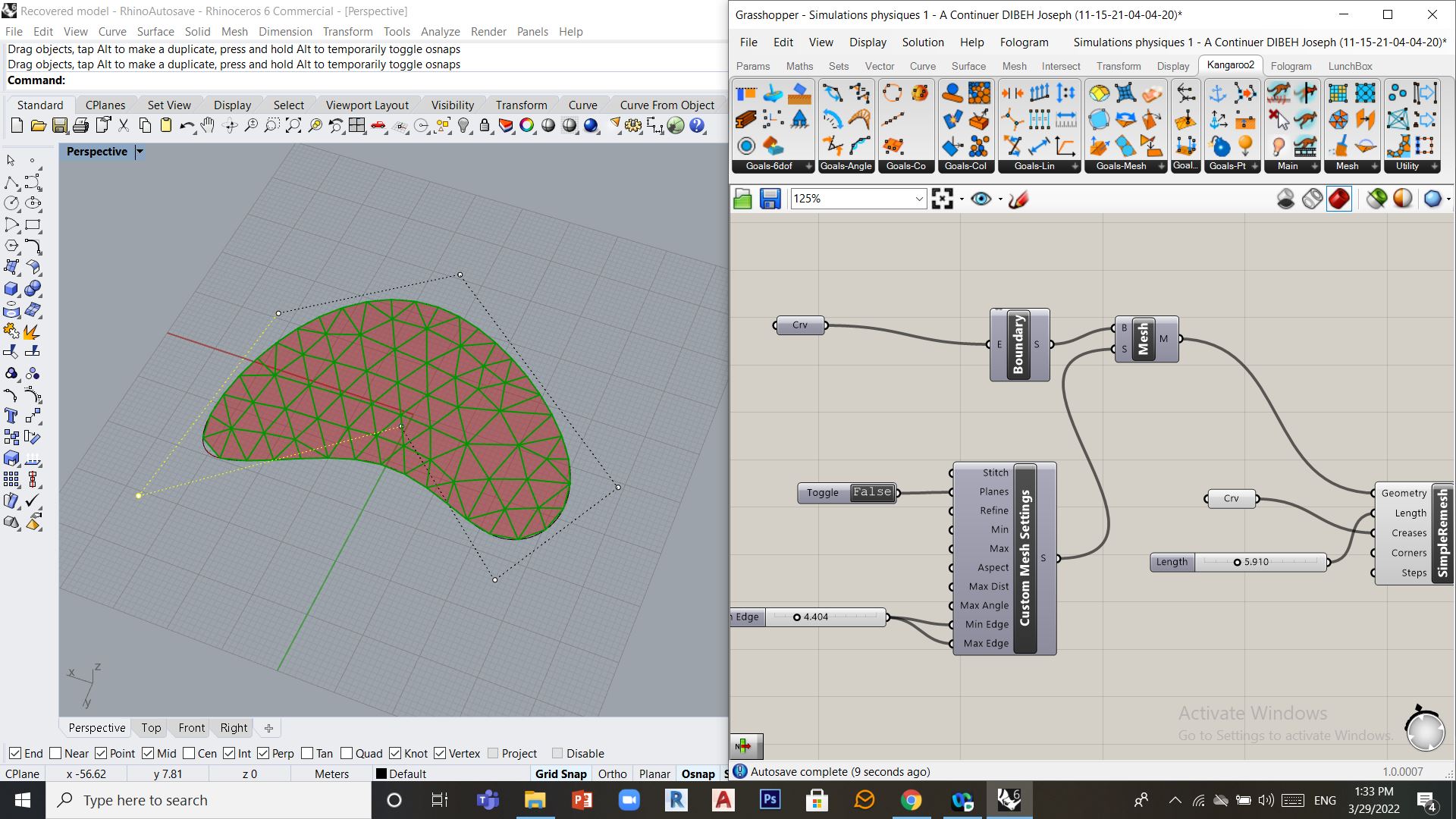
On peut ensuite soumettre ce maillage à des contraintes physiques en utilisant Kangaroo c-à-d on continue comme les exemples précédents.
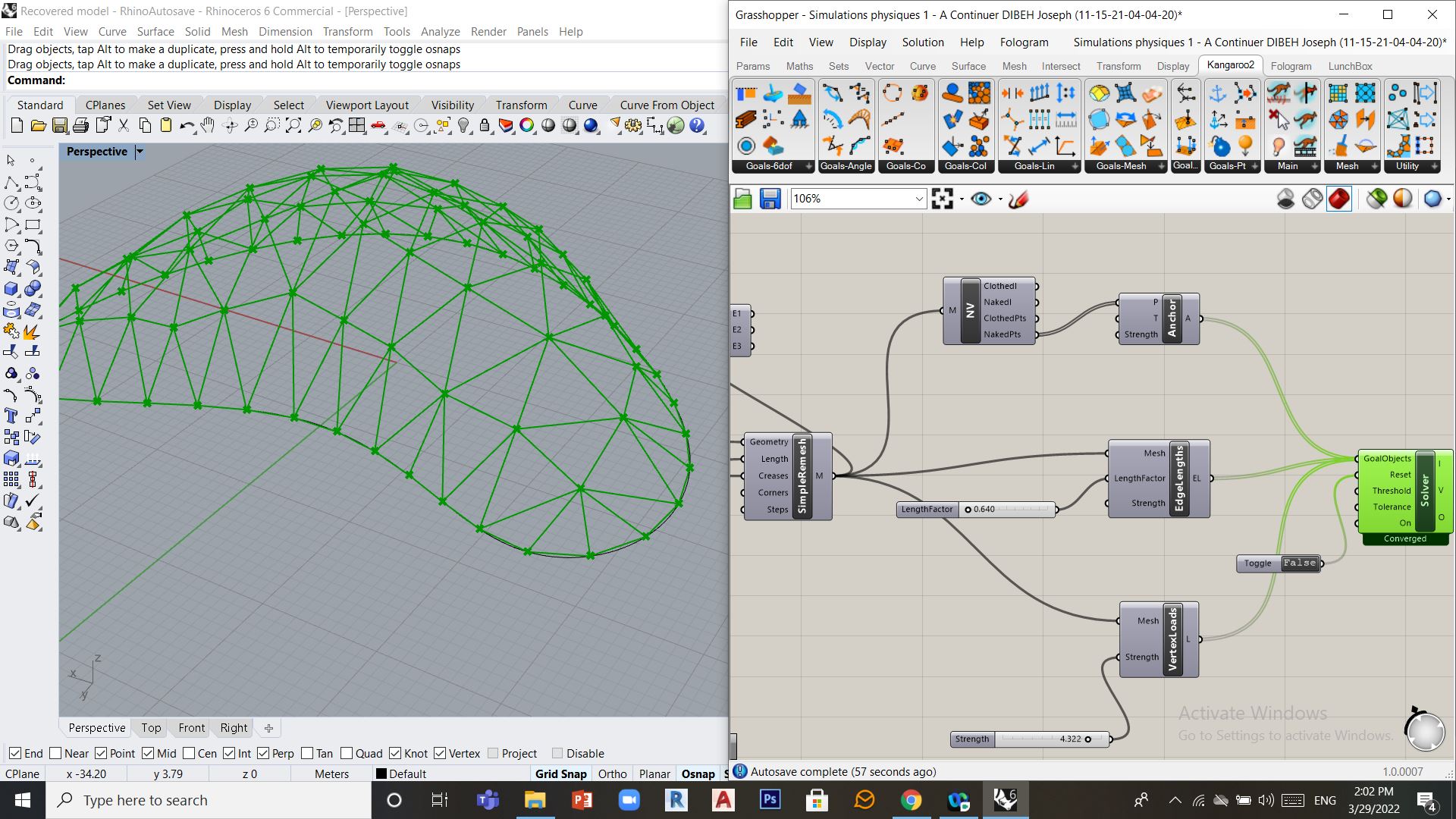
Pour pouvoir entrer dans cet espace on peut fixer des contraintes d’ancrage que sur certains points contour. Pour sélectionner la partie du contour à ancrer au sol on peut utiliser un composant Series (Set/Sequences/Series) qui produit une série de valeurs à partir d’un entier de départ. Cet entier correspond à l’indice du point de départ de l’ancrage du contour. L’entrée Count permet de définir le nombre de points suivants à ancrer. Munis de cette liste d’indices de points du contour, le composant List Item (Set/List/List Item) en produit les coordonnées qui sont utilisées par le composant Anchor (Kangaroo2/Goals-Pt/Anchor) pour créer les contraintes d’ancrage.
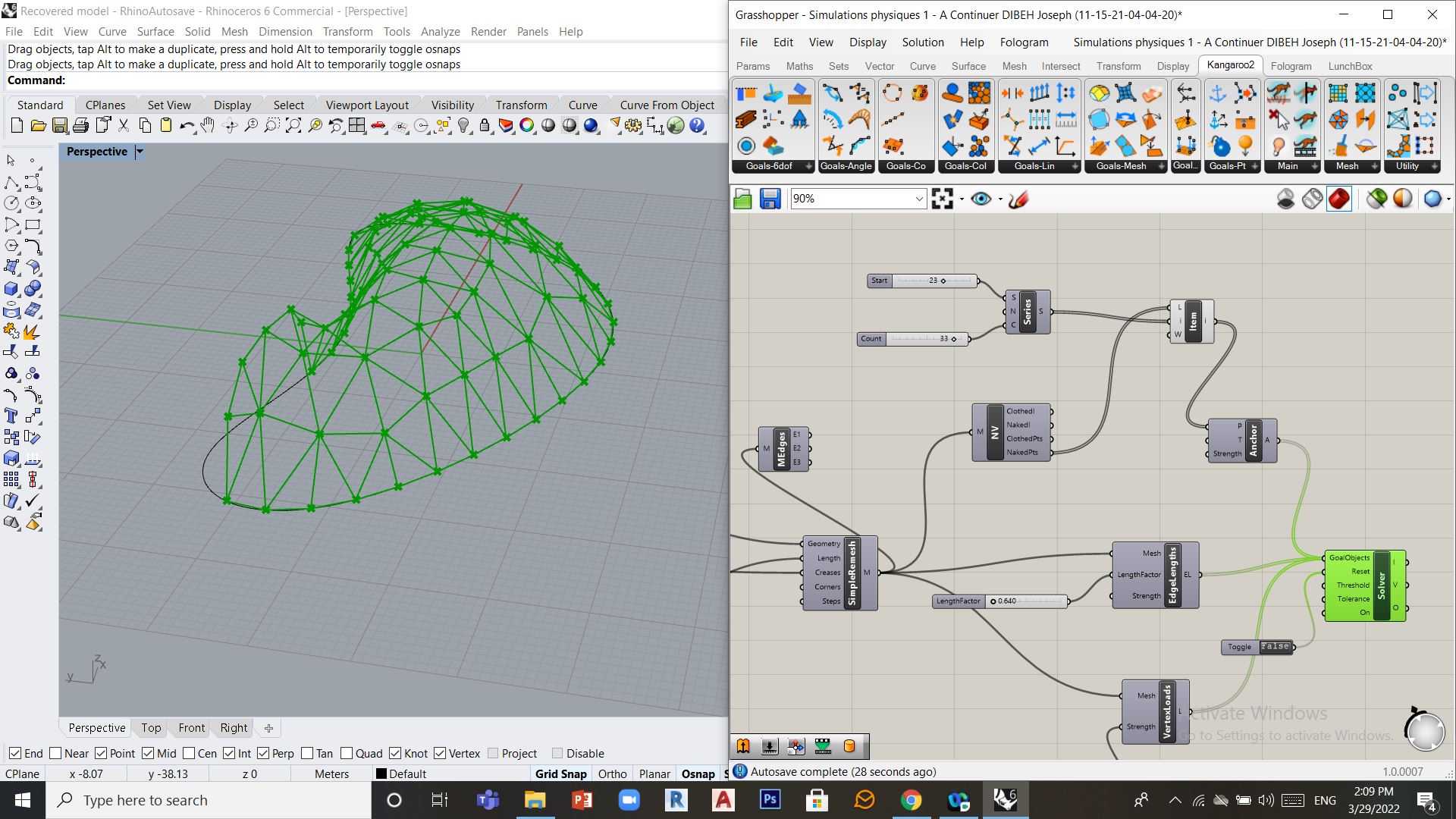
Exemple 1: couvrir une espace complexe avec des voutes
Il s’agit dans cet exemple de couvrir avec des voutes une zone formée de 4 hexagones.
1 – Création du maillage isotrope en hexagone
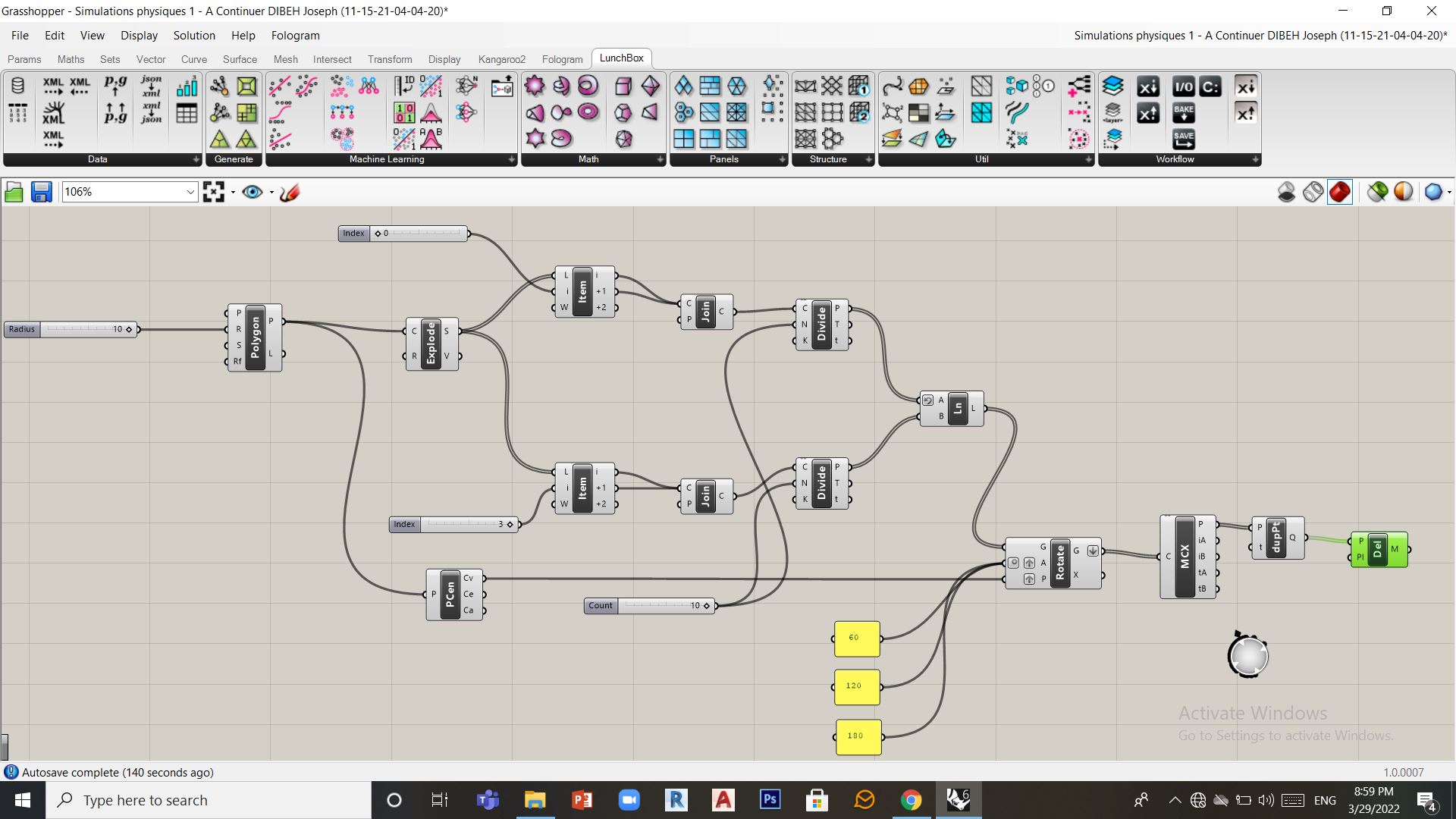
2 – Recherche de forme
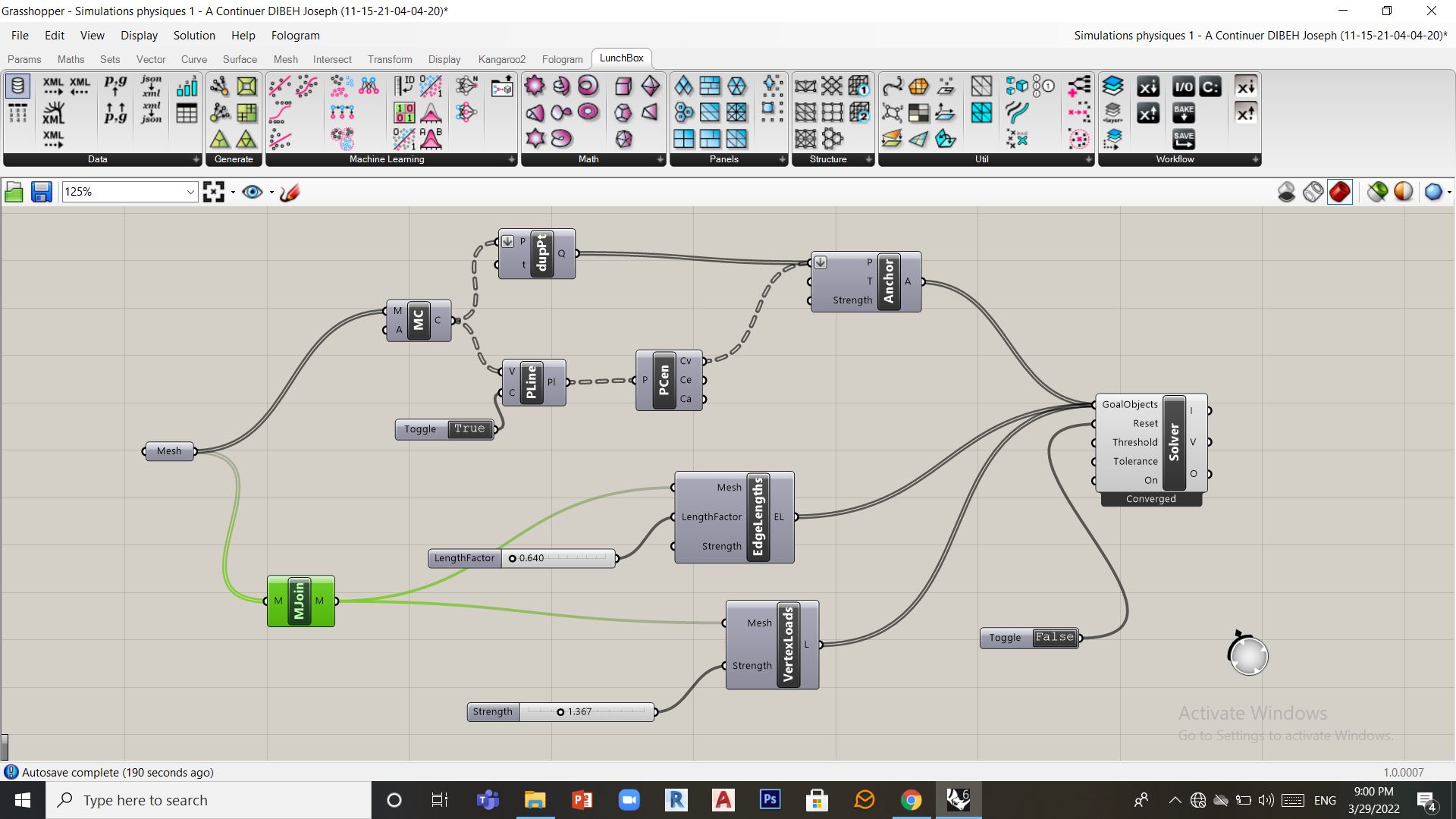
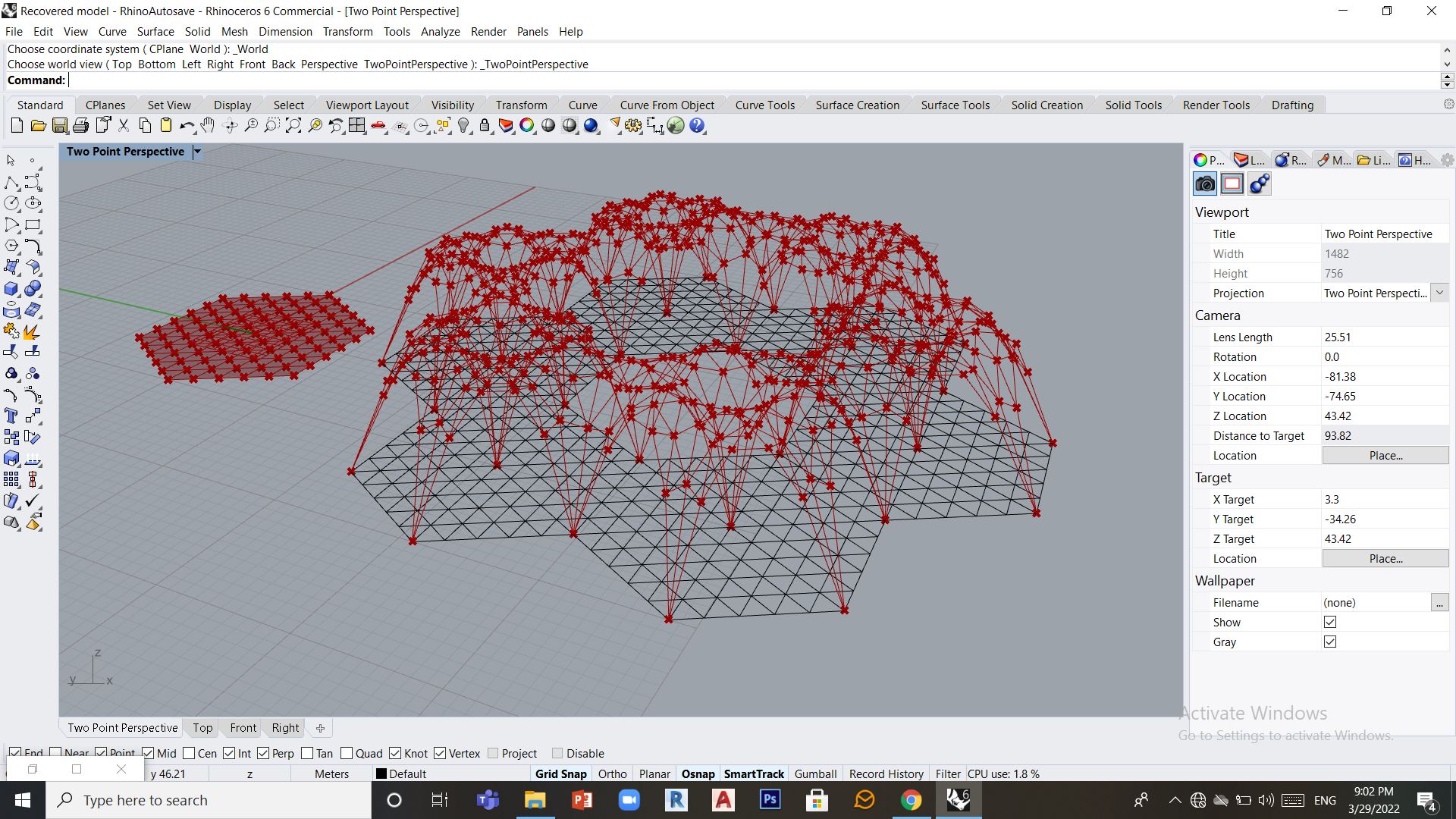

1 comment
François Guéna says:
Mar 30, 2022
Bon travail, bien décrit.