LA CURBE DU CRABE
Étape 1
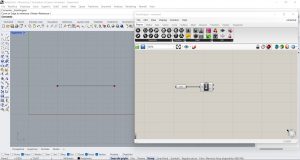
J’ai commencé par dessiner un segment dans Rhino et l’associer au composant Courbes (Params/Geometry). J’ai ensuite inséré le paramètre End Curve (Curve/Analysis) pour identifier les extrémités du segment. La sortie S représente l’extrémité d’origine et la sortie E représente l’extrémité de fin.
Étape 2
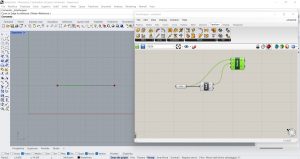
J’entre le paramètre Scale (Transform/Affine) pour pouvoir appliquer au segment une transformation homothétique avec le centre l’origine de la ligne.
Étape 3
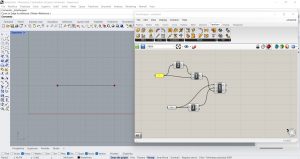
Pour calculer la racine 2 pour 2, j’ai inséré trois composants : un Panel (Params/Input), un Square Root (Maths/Polynominal) et un Division (Maths/Operators). J’ai connecté le Panel à l’entrée x du Square Root et à l’entrée B de la Division. La sortie du Square Root à l’entrée A de la Division. La sortie R du paramètre Division produit la racine 2 pour 2.
Étape 4
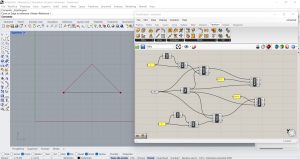
Insérer un composant Rotate (Trasform/Euclidean) pour appliquer une rotation à la ligne avec centre S et angle pi/4.
J’ai appliqué les mêmes étapes à l’extrémité E du segment et j’ai obtenu une forme presque triangulaire. J’ai ensuite connecté un paramètre Courbes aux deux sorties G des composants Rotate.

Étape 5
Pour réappliquer récursivement le programme, j’ai installé un plug-in Grasshopper appelé Anemone. J’insère un composant Loop Start (Anemone/Class) et un composant Loop End (Anemone/Class) pour planifier le début et la fin du traitement récursif à exécuter.
Je connecte à l’entrée N un curseur pour vérifier le nombre de répétitions du schéma, à l’entrée T un bouton Boolean pour activer ou désactiver la répétition et à la sortie D0 la ligne de départ de Rhino. Je connecte la sortie principale du Loop Start à l’entrée mineure du Loop End et la sortie D0 du Loop Start à la première courbe insérée au début de l’exercice et la sortie D0 du Loop End à la courbe insérée à la fin de l’étape 4.
AUTRE EXEMPLES:
La courbe du dragon
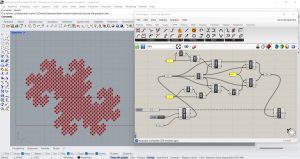
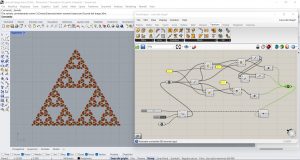
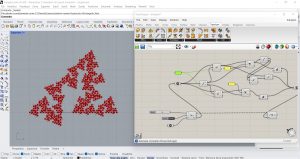
Le triangle de Sierpisky

1 comment
François Guéna says:
May 8, 2022
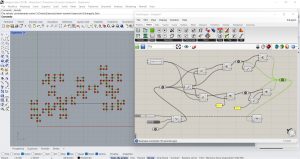
Même problème ici que pour les étudiants qui ont déposé leur article précédemment. Pour le triangle de Sierpinsky la règle de substitution nécessite 3 transformations. Je n’en distingue que 2 sur les images du code. Pour la courbe suivante il faut 4 transformations et pour la dernière 7 transformations.